résolution d'inéquations

[chat]

Bonjour,

exercice : Résoudre dans l'ensemble des nombres réels les inéquations en prenant soin de déterminer auparavant les éventuelles valeurs interdites.

b. (-x+5)² > (-2x+1)²
(-x+5)² - (-2x+1)² > 0
[(-x+5) + (-2x+1) ] [(-x+5) - (-2x+1)] > 0
[ - x + 5 - 2x + 1 ] [ -x + 5 + 2x - 1 ] > 0
(-3x + 6 ) ( x + 4) > 0

-3x + 6 = 0
-3x = -6
x = -6/-3 = 6 /3 = 2

Ici a = -3
donc a < 0

x + 4 = 0
x = -4

Ici a = 1
donc a > 0

Tableau de signes :

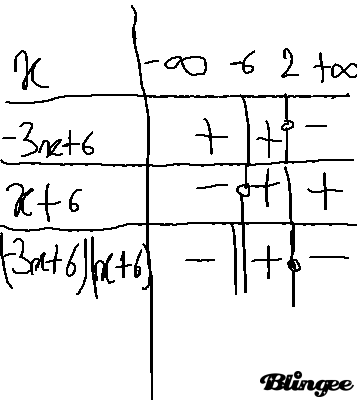
Je me suis trompé il faut juste changer le -6 dans la première ligne( la ligne où il y a x) et mettre -4 et dans la 3 ème ligne à la place de x + 6 c'est x + 4 et dans la dernière ligne dans le produit : (-3x+6) (x+6) c'est (-3x +6) (x+4).

On cherche les réels x tels que (-3x+6) (x+6) > 0. On cherche donc les valeurs de x qui rendent le produit strictement positif. On lit dans le tableau : S = ] -6 ; 2 [

Pouvez vous me dire si mes réponses sont bonnes s'il vous plait. Merci.

[mtschoon]

Bonjour ,

Jusqu'à "(-3x + 6 ) ( x + 4) > 0" c'est bon

Ta démarche pour trouver les signes est bonne aussi.

Dans les valeurs du tableau , vu les erreurs , il faut refaire... la double barre n'a pas de sens vu qu'il y a un produit...on n'y comprend rien.

Ay final , après modifications , tu devrais trouver ]-4 ,2[