fonction trinome ( chute de pierre )

Bonsoir j'aimerais savoir si ce que j'ai fait est juste et j'aimerais avoir des explications pour ce que je n'ai pas compris.

Adam, un garçon de 1.40 m, lance verticalement et vers le haut une pierre avec une vitesse initiale de 9.1m/s. Soit $t$ le temps écoulé, en seconde, à partir de l'instant où Adam lâche le caillou. En négligeant la résistance de l'air, on admet que la hauteur au sol $H$ de la pierre, en mètres, est une fonction définie par $H(t) = -4,9t^2+9,1t+1,4$ .

Montrer qu'Adam lâche la pierre à hauteur de sa tête.

Je ne comprend pas, pouvez-vous m'expliquer. :frowning2:

Montrer que pour tout réel t, $-\frac{1}{10}(7t-14)(7t+1)$ .

$−110(7t−14)(7t+1)=−4,9t2+9,1t+1,4-\frac{1}{10}(7t-14)(7t+1) = -4,9t^2+9,1t+1,4$
$=−110(49t2+7t−98t−14)=-\frac{1}{10}(49t^2+7t-98t-14)$
$=−110(49t2−91t−14)=-\frac{1}{10}(49t^2-91t-14)$
$4,9t^2+9,1t+1,4$

Est-ce juste

Au bout de combien de temps la pierre retombe-t-elle au sol ?

Je ne comprends pas, pouvez-vous m'expliquer. :frowning2:

Sur l'intervalle [0;2] tracer dans un repère orthogonal la courbe représentative de la fonction $H$ . On prendra 5cm pour 1s en abscisse et 2 cm pour 1m en ordonnée.

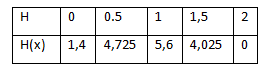
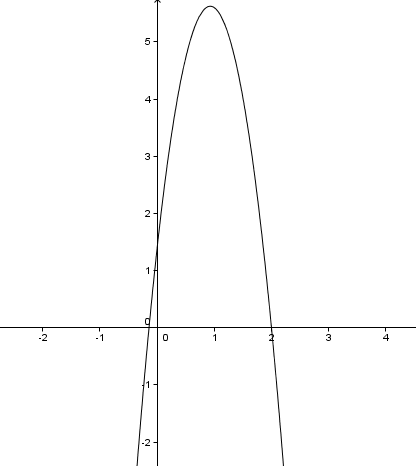
$fichier math$

a) Dresser graphiquement le tableau de variations de la fonction $H$ sur [0;2].

$\begin{tabular}{|c|ccccccc|}x&0&&1&&2&& \ \hline \ \{H}&&\nearrow&&\searrow&&\ &1.4 &&5.6&&0&\end{tabular}$

Est-ce juste

b) Déterminer graphiquement le maximum de $H$ sur [0;2].

Graphiquement le maximum de $H$ sur [0;2] et 5,6.

Est-ce juste

c) En déduire la hauteur la plus élevée atteinte par la pierre et le temps qu'elle a mis pour l'atteindre.

La hauteur la plus élevée atteinte par la pierre est 5.6 mètres de hauteur et le temps qu'elle a mis pour l'atteindre est 1 seconde.

Est-ce juste

Déterminer algébriquement après combien de temps Adam risque de recevoir la pierre sur la tête (donner la valeur exacte ainsi que la valeur approché au centième).

Je ne comprends pas, pouvez vous m'expliquer :frowning2:

Merci beaucoup pour votre aide

Pouvez-vous m'aider SVP

Bonjour,

Je regarde le début,

Pour t=0 , H(t)=1.4 donc.................
Si une vérification suffit , c'est bon
Tu dois résoudre H(t)=0

Bonjour mtschoon,

Donc comme H(t)=1.4, on prouve qui lâche la pierre à la hauteur de sa tête car le garçons mesure 1.40 mètres.

3) $−110(7t−14)(7t+1)=0-\frac{1}{10}(7t-14)(7t+1)=0$

Un produit est nul si l'un ou moins des facteurs est nul.

7t-14=0
7t=14
t=2

7t+1=0
7t=-1
t=-1/7

Donc la pierre retombe au sol au bout de 2 secondes.

oui.

Et pour t = -1/7 on en fait quoi mtschoon ?

Et la suite semble correct ?

Merci

t=-1/7 ne convient pas vu que la chute commence à t=0

L'énoncé précise que le graphique doit être fait sur l'intervalle [0;2] ( temps correspondant à la chute ) , il faut donc que tu supprimes ce qui ne convient pas.

Ok merci pour ton explication mtschoon c'est plus clair dans ma tête.

Et pour la question 6. pourrais-tu m'expliquer.

Merci beaucoup

Adam mersure 1.40m.

Alors , pense à quelle hauteur doit se trouver la pierre (lorsqu'elle retombe ) pour que Adam la recoive sur la tête (* s'il n'a pas eu l'idée de changer de place.*.. )

Si on regarde le graphique il devrait la recevoir au bout de 1.9 secondes mais ce n'est pas précis.

Non , avec le graphique ce n'est pas précis , mais l'énoncé te dit de le faire ALGEBRIQUEMENT

Faudrait résoudre H(t)=1.40

OUI.

-7/10t+7/5=1.4
-7/10t=0
t=0

-7/10t-1/10=1.4
-7/10t=3/2
Après je bloque pour résoudre l'équation.

Ta démarche est fausse .
Elle ne s'applique que pour un produit de facteurs égal à 0

Utilise l'expression du début de l'énoncé.

$4.9t^2+9.1t+1.4=1.4$
$4.9t^2+9.1t=0$

Après je n'arrive pas à résoudre avec le t²

Ou ca serait l'équation du second degré ?

Donc $t (- 4.9 t + 9.1) = 0$

t=0

ou

-4.9t+9.1=0
-4.9t=-9.1
t=13/7 ou 1.86

Adam risque de recevoir la pierre sur la tête au bout de 13/7 secondes (valeur exacte) ou 1.86 secondes ( valeur approchée au centième)

C'est bon ( et bien sûr , tu supprimes t=0 qui est l'instant du lancement de la pierre )

Ok merci mtschoon, le reste semble correct autrement ?

Si tu as modifié les points que je t'ai précisés , cela semble correct.

Fais une bonne rédaction , bien sûr.

mtschoon
Si tu as modifié les points que je t'ai précisés , cela semble correct.

Le 1.; 3. et le 6. ?

Ne vous inquiétez pas pour la rédaction :razz:

Et la courbe de la 4) car t ∈[0,2]

Oui merci mtschoon, là je ne pouvais pas le faire vue que c'était avec un logiciel mais merci de me le rappeler.

Bonne fin de journée à vous.