Angle dans un pavé
-
NNessaah dernière édition par
Bonjour, Je suis bloqué sur un exercice, j'aimerais beaucoup qu'on m'aide
Soit ABCDEFGH un pavé tel que AB = AE = 1 cm et AD = 2 cm. Soit M un point mobile sur le segement [BC]. On notera x la distance BM en centimetres. On admettra que ,quelle que se soit la position du point M sur [BC], le triangle EAM est rectangle en A. On s'interesse aux valeurs prises par la mesure de l'angle a= EMA selon les valeurs de x.
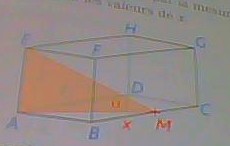
- Quelle est la valeur de a si x = 0? si x = 2 ?
-
Mmathtous dernière édition par
Bonjour,
Commence par calculer AM.
-
NNessaah dernière édition par
Comment calculer AM si je n'ai pas la valeur de EM ?
-
Mmathtous dernière édition par
S'agit-il d'un pavé "droit" ?
Si oui, quelle est la nature du triangle ABM ?Pour x=0, où est M ?
-
NNessaah dernière édition par
Non, ce n'est pas un pavé droit, car, un pavé droit possède seulement des faces rectangulaire alors que nous nous avons un pavé avec 4 faces rectangulaire et 2 faces carrés mais sachant que la face ABCD est un rectangle le triangle ABM est un triangle rectangle en B
-
Mmathtous dernière édition par
Il s'agit donc bien d'un pavé droit car les carrés sont des rectangles.
ABM est rectangle en B (sauf si x = 0). Tu peux donc calculer AM.
Pour x=0, où est M ?
-
NNessaah dernière édition par
M sera a la place de B
-
Mmathtous dernière édition par
Dans ce cas, quelle est la nature du triangle ABE (ou AME puisque M = B) ?
-
NNessaah dernière édition par
C'est un triangle rectangle en A
-
Mmathtous dernière édition par
Pas seulement, il est aussi ...?
-
NNessaah dernière édition par
Isocèle, les cotés AE et AB sont égaux
-
Mmathtous dernière édition par
Oui, quelle est alors la mesure de l'angle a ?
-
NNessaah dernière édition par
Sachant qu'un triangle rectangle isocèle possède un angle droit de 90° et deux angles de 45°
-
Mmathtous dernière édition par
Termine ta phrase : a mesure donc 45°.
Revenons maintenant aux cas où x > 0 : le triangle ABM existe et est rectangle en B. Tu peux donc calculer AM.
-
NNessaah dernière édition par
Pour x = 2
Je me place dans le triangle ABM rectangle en B
Le théorème de Pythagore donne
AM² = AB² + BM²
AM² = 1² + 2²
AM² = 1 + 4
AM² = 5
donc AM = √5
-
Mmathtous dernière édition par
C'est juste.
Que vaut alors l'angle a ?
Pour cela, tu peux utiliser une fonction trigonométrique de cet angle.
-
NNessaah dernière édition par
J'utilise la tangante donc, coté opposé/coté adjacent
ce qui donne :
tan EMA = EA/AM
tan EMA = 1/√5
EMA ≈ 24.09°
-
Mmathtous dernière édition par
C'est juste.
S'il y a d'autres questions, il va bien falloir maintenant calculer AM (en fonction de x).
-
NNessaah dernière édition par
Il n'y a pas d'autre question, la suite est une lecture graphique assez simple, merci beaucoup de ton aide.
-
Mmathtous dernière édition par
De rien.
Bon courage.