Calcul de la hauteur et l'aire des faces d'une pyramide a base carrée
-
NNessaah dernière édition par Hind
Bonjour, Je suis bloqué dans cette exercice.
Une pyramide SABCD a pour base un carré de 10 cm de côté. Les faces latérales sont des triangles équilatéraux.
- Calculer la hauteur de SH de la pyramide
- Calculer l'aire totale des faces de la pyramide
3.Si E est le milieu de [SC], montrer que la droite (SC) est perpendiculaire au plan (DEB) - Calculer l'aire du triangle DEB
J'ai fais le shéma suivant :
Pour le 1 j'ai raisonner ainsi :
Sachant qu'un carré a ses diagonales de même longueurs, qui se coupent en leurs milieu et qui sont perpendiculaire.
Je me met dans le triangle ADC rectangle en D
Le théoreme de Pythagore donne :
CA² = AD² + CD²
CA² = 10² + 10²
CA² = 200
CA = √200 = 10√2 cm
Je sais que AH est la moitié de CA donc, 10√2 / 2 = 5√2 cm
Donc, AH = 5√2 cm
Dans le triangle AHS rectangle en H
Le théoreme de Pythagore donne :
AS² = AH² + SH²
SH² = AS² - AH²
Sachant que c'est un triangle équilatérale AS = AB = 10cm
Donc, SH² = 10² - (5√2)²
SH² = 100 - 50 = 50
SH = √50 = 5√2
Ce qui fait que la hauteur est égale à la moitié de la longueur d'une diagonale, est ce normale ?
-
Mmathtous dernière édition par
Bonjour,
Oui, rien d'anormal.
Tout dépend de la forme de la pyramide.
-
NNessaah dernière édition par
Nous n'avons pas de figure, donc, mon raisonnement ai juste ? la hauteur mesure bien 5√2 cm ?
-
Mmathtous dernière édition par
Oui.
La figure est celle que tu as donnée.
-
NNessaah dernière édition par
Oui, maintenant pour calculer l'aire totale des faces de la pyramide donc la question 2, mon raisonnement est le suivant :
Je sais que l'aire totale d'un solide est la somme de l'aire latérales et des aides de bases donc,
l'aire d'un triangle = (bxh) / 2
donc, ici A = ( 10 x 5√2 ) /2
A = 25√2 cm²
l'aire d'un carré = cxc
donc ici, A = 10 x 10
A = 100 cm²
Donc pour trouvé l'aire totale je fais, aire faces latérales + aires bases
donc ici, Atotal = 25√2 x 4 + 100
Atotal ≈ 241,42 cm²
-
Mmathtous dernière édition par
Non.
Précise ce que tu entends par A,b, et h.
N'oublie pas que les faces latérales sont des triangles équilatéraux.
-
NNessaah dernière édition par
L'aire d'un triangle équilatérale est le suivany : A = c * √c² - (c/2)² / 2 ?
-
Mmathtous dernière édition par
Non.
Dessine un triangle équilatéral, ici de côté 10, et trace l'une de ses hauteurs : il faut calculer la longueur de cette hauteur.
-
NNessaah dernière édition par
la hauteur du triangle joint un sommet au milieu du cote oppose. Dans le triangle SDO rectangle O.
Le theoreme de Pythagore donne :
SD² = SO² + DO²
SO² = SD² - DH²
SO² = 10² - 5²
SO² = 75
√75 = 5√3 cm
donc, SO = 5√3 cm
Je sais que l'aire totale d'un solide est la somme de l'aire latérales et des aides de bases donc,
l'aire d'un triangle = (bxh) / 2
donc, ici A = ( 10 x 5√3 ) /2
A = 25√3 cm²
l'aire d'un carré = cxc
donc ici, A = 10 x 10
A = 100 cm²
Donc pour trouvé l'aire totale je fais, aire faces latérales + aires bases
donc ici, Atotal = 25√3 x 4 + 100
Atotal ≈ 273,20 cm²
-
Mmathtous dernière édition par
Garde le résultat exact. Ne donne de valeurs approchées que si on te le demande.
Ici, écris Atotal = 25√3 x 4 + 100 = 100√3 + 100
-
NNessaah dernière édition par
Si E est le milieu de [SC], montrer que la droite (SC) est perpendiculaire au plan (DEB)
comment montrer cela ?
-
Mmathtous dernière édition par
Si tu es gêné par le dessin en perspective, fais des dessins séparés des faces SBC et SCD.
Que peut-on dire des droites (BE) et (SC) ?
-
NNessaah dernière édition par
(BE) est perpendiculaire a (SD)
-
Mmathtous dernière édition par
Tu veux dire à (SC) ?
-
NNessaah dernière édition par
Oui voilà pardon
-
Mmathtous dernière édition par
Et si tu regardes l'autre face : SCD : que peux-tu dire ?
-
NNessaah dernière édition par
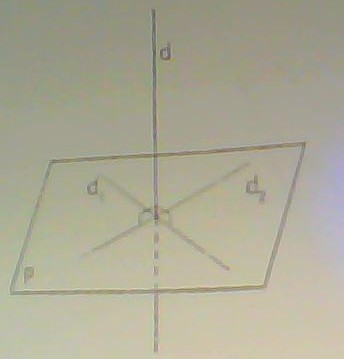
Je connais une propriété qui dis :
On dit que la droite d est perpendiculaire au plan P si elle est perpendiculaire à deux droites sécantes de P.
Dans ce cas, d est perpendiculaire à toute droite du plan P.
-
Mmathtous dernière édition par
Oui, c'est cette propriété qu'il va falloir utiliser.
Mais avant, tu dois donner deux droites du plan (EBD) perpendiculaires à ta droite (SC) : pour le moment tu n'en as cité qu'une : (BE).
-
NNessaah dernière édition par
(BE) est perpendiculaire a (SD)
-
Mmathtous dernière édition par
Non.
Dans le triangle équilatéral SBC, (BE) est perpendiculaire à (SC).
Dans le triangle équilatéral SCD, (DE) est perpendiculaire à (SC).
Les droites (BE) et (DE) sont deux droites du, plan EBD, sécantes (en E) et perpendiculaires à (SC), donc selon la propriété que tu as rappelée, (SC) est perpendiculaire au plan EBD.
-
NNessaah dernière édition par
Comment calculer l'aire du triangle DEB ?
-
Mmathtous dernière édition par
Calcule EH.
-
NNessaah dernière édition par
Je n'arrive pas
-
Mmathtous dernière édition par
Suis le conseil que je t'ai déjà donné : dessine à part le triangle SHC.
Quelle est sa nature ?
-
NNessaah dernière édition par
C'est un triangle rectangle
-
Mmathtous dernière édition par
Pas seulement, souviens-toi de ta première question.
-
NNessaah dernière édition par
Rectangle et isocèle
-
Mmathtous dernière édition par
Oui, alors que vaut EH ?
-
NNessaah dernière édition par
5√2
-
Mmathtous dernière édition par
Non.
Dessine SHC, tu verras que ta réponse est forcément fausse.
-
NNessaah dernière édition par
C'est 5√2 / 2
-
Mmathtous dernière édition par
Non.
SHC est rectangle et isocèle en H.
SH = HC = 5√2
SC = 10.
E est le milieu de [SC] ...
-
NNessaah dernière édition par
Donc, EH vaut 5
-
Mmathtous dernière édition par
Oui.
Maintenant, dessine le triangle EBD. Quelle est sa nature ?
-
NNessaah dernière édition par
Rectangle et isocèle aussi
-
Mmathtous dernière édition par
Non : je ne suis pas sûr qu'il soit rectangle. Mais isocèle, oui car BE = DE : regarde les deux triangles équilatéraux SBC et SCD, de même "taille".
-
NNessaah dernière édition par
Je n'arrive pas
-
Mmathtous dernière édition par
Tu es fatigué, voilà tout.
J'espère que ton exercice n'est pas pour demain ?
-
NNessaah dernière édition par
Si mais j'y suis depuis 1semaine
-
Mmathtous dernière édition par
Est-ce que tu comprends que EBD est isocèle ?
EB = ED = 5√3 ( la hauteur des faces équilatérales).
De toute façon inutile de connaître leur valeur.
Car H est le milieu de [BD]et donc EH est la hauteur du triangle EBD, BD étant la base.
Tu peux donc calculer l'aire de ce triangle.