étude de fonction polynome

soit la fonction définie sur l'intervalle [10 ;25] par:
f(x)=-x³+30x²-153x

déterminer la fonction dérivée f' de la fonction f.vérifier que :
f '(x)=3(x-3)(17-x).
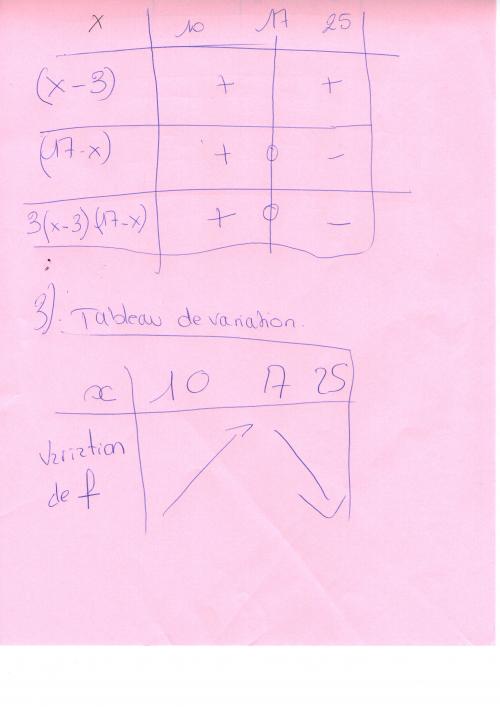
2)étudier le signe de la fonction f' sur l'intervalle [10 ;25].
3)en déduire le tableau de variation de la fonction f sur l'intervalle [10 ;25].
déterminer une équation de la tangente au point d'abscisse 10
déterminer une équation de la tangente au point d'abscisse 25
tracer la courbe représentative de la fonction f ainsi que les 2 tangentes.
voici mon travaille
$1)f(x)=x^3$ +30 x²-153x
f'(x)=3x²+302x-1531
f'(x)=3(x-3)(17-x)
f'(x)=3x+3(-3)+317+3(-x)
f'(x)=(3x-9)+(51-3x)

Bonsoir

la première expression de f'(x) est bonne

Tes deux dernières lignes de calcul sont à revoir

3(x-3)(17-x)=3(x-3)=3x-9

Tu continues en distribuant , tu simplifies et tu dois trouver l'expression de f'(x) précédente.

3(x-3)(17-x)=3(x-3)=3x-9
-3x²+60x-153
donc ici je simplifie se qui me donne f'(x)=3(x-3)(17-x)
2.étude du signe de f'
tu as démontré en 1. que f'(x)=3(x-3)(17-x)
étudie le signe du produit 3(x-3)(17-x),composé de 3 facteurs, dans un tableau de signes
le facteur 3 est toujours >0
facteur (x-3)=0 quand x=3 positif si x>3 et négatif si x<3
apres je vois plus

facteur (17-x)=0 quand x=17 positif si x>17
négatif si x>17

Tu as dû te tromper en écrivant.

(17-x) positif pour x < 17

tu travailles sur l'intervalle [10,25] , x > 17 , donc (17-x) négatif

je peux passer a la question 3

je suis perdu n'arrive pas a faire mon tableau de variation

Tu travailles seulement sur [10,25]

3 positif
x-3 positif
17-x positif pour 10 ≤ x < 17 , 17-x nul pour x=17 et 17-x négatif pour 17 < x ≤ 25

Donc f'(x) positive pour 10 ≤ x < 17 , nulle pour x=17 et négative pour 17 < x ≤ 25

je comprend rien désolé moi j'avais mis sur
une ligne
x -∞ 17 3 +∞
(x-3)
(17-x)
3(x-3)(17-x)

Relis ton énoncé .

x ne varie pas entre -∞ et +∞ ,il varie entre 10 et 25

Il faut faire un tableau avec x variant entre 10 et 25
Si tu le fais entre -∞ et +∞ , il faudra barrer tout ce qui est inférieur à 10 et tout ce qui est supérieur à 25 .

( en plus , 3 n'est pas entre 17 et +∞ )

donc si je comprend sur ma ligne de x 10 25
puis en dessous de x (x-3)
(17-x)
3(x-3)(17-x)

Oui , et sur la ligne des x , entre 10 et 25 , marque 17

voici mon tableau de variation

$fichier math$

donc si je résume mon exercice
1)déterminer
f(x)=x³+30x²-153x
f'(x)=3x²+302x-1531
3(x-3)(17-x)=3(x-3)=3x-9
-3x²+60x-153
donc ici je simplifie se qui me donne f'(x)=3(x-3)(17-x)
2.étude du signe de f'
f'(x)=3(x-3)(17-x)
étudie le signe du produit 3(x-3)(17-x),composé de 3 facteurs, dans un tableau de signes
le facteur 3 est toujours >0
facteur (x-3)=0 quand x=3 positif si x>3 et négatif si x<3
donc (x-3) positif
17-x positif pour 10 ≤ x < 17 , 17-x nul pour x=17 et 17-x négatif pour 17 < x ≤ 25

Donc f'(x) positive pour 10 ≤ x < 17 , nulle pour x=17 et négative pour 17 < x ≤ 25
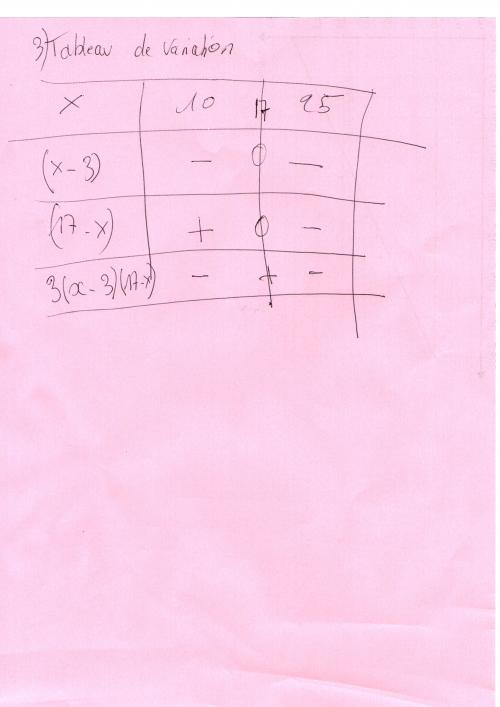
3) tableau de variation

Dans ton tableau , la ligne de (x-3) est fausse : il faut des "+" ( car x est plus grand que 3 )

La dernière ligne se retrouve donc fausse ( et mets un "0" pour x=17 )

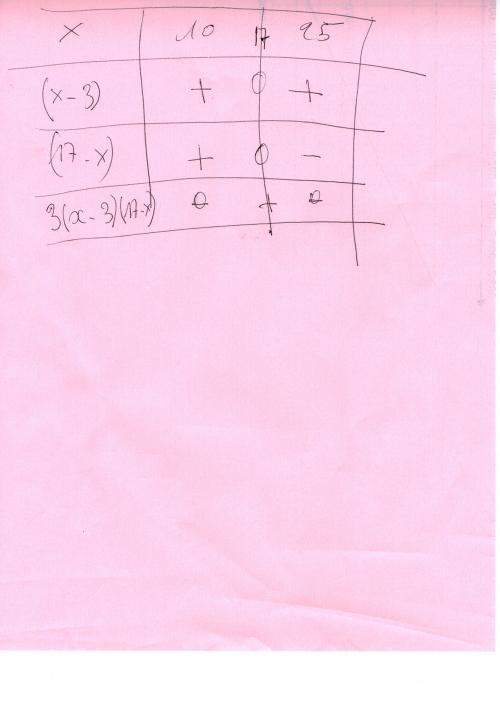
voila j'ai fait ma correction de mon tableau la présentationest bien faite comme cela $fichier math$

Je ne conprends pas ta dernière ligne.

Il faut "+" , puis 0 ( sur la barre de x=17 ) , puis "-"

donc j'ai refait mon tableau car j'avais fait ma correction dessus

$fichier math$

tu n'as pas compris x=17

Pour x=17 tu mets fais un trait vertical et tu mets "0" à cheval sur le trait à la seconde et la 3eme ligne
( c'est la méthode usuelle )

peux tu me dire si mon exercice est bon
1)déterminer
f(x)=x³+30x²-153x
f'(x)=3x²+302x-1531
3(x-3)(17-x)=3(x-3)=3x-9
-3x²+60x-153
donc ici je simplifie se qui me donne f'(x)=3(x-3)(17-x)
2.étude du signe de f'
f'(x)=3(x-3)(17-x)
étudie le signe du produit 3(x-3)(17-x),composé de 3 facteurs, dans un tableau de signes
le facteur 3 est toujours >0
facteur (x-3)=0 quand x=3 positif si x>3 et négatif si x<3
donc (x-3) positif
17-x positif pour 10 ≤ x < 17 , 17-x nul pour x=17 et 17-x négatif pour 17 < x ≤ 25
Donc f'(x) positive pour 10 ≤ x < 17 , nulle pour x=17 et négative pour 17 < x ≤ 25
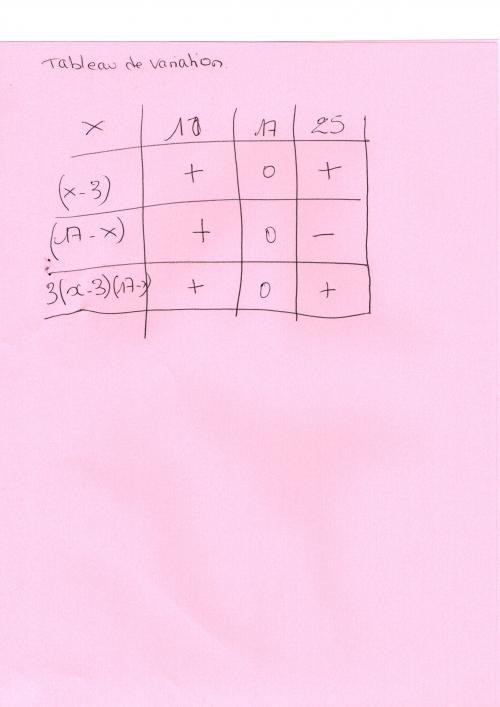
3) tableau de variation

$fichier math$

Presque juste , sauf la case de droite de la dernière ligne

par - donne -

Mais , ce ci n'est pas le tabeau de varietion , c'est le tableau de signes de la dérivée.

Il faut que tu complètes ou que tu fasses un nouveau tableau avec signe de f'(x) et sens de variation de f :

f croissante entre 10 et 17
f décroissante entre 17 et 25

voici la correction de mon tableau de signe de la dérivée est de mon tableau variation $fichier math$

Oui mais en principe on met entre x et f une ligne pour le signe de f'(x)

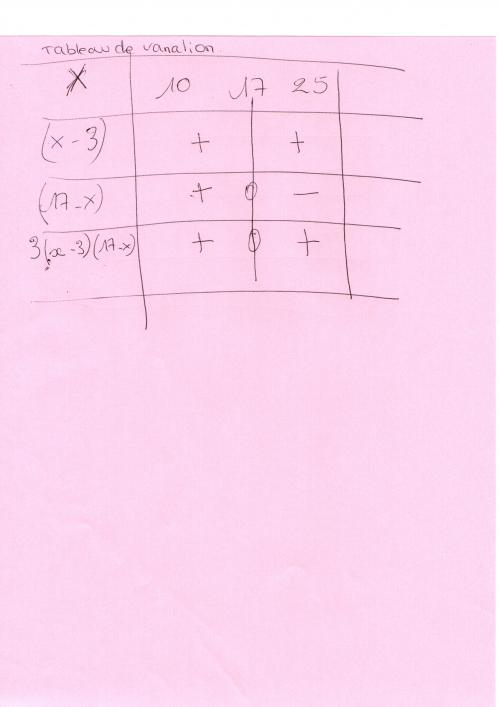
donc j'ai corrigé mon tableau le voici 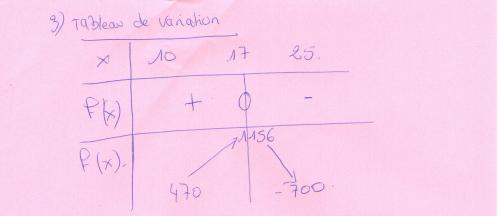$fichier math$ apres mon tableau peux tu me dire si mes tangentes sont bonne merci d'avance
4) tangente au point d'abscisse 10
y=f'(x0)(x-x0)+f(x0)
y= f'(10)(x-10)+f(10)
y=470
ou comme cela
y= f(10)x+b
y=470x+b
10=47010+b
10=4700+b
10-4700=b
-4699=b
y=10x-4699
5)tangente au point d'abscisse 25
y=f(25)x+b
y=-700x+b
25=-70025+b
25=-17500+b
25+17500=b
17525=b
y=25x+17525
ou
y=f'(x0)(x-x0)+f(x0)
y= f'(25)(x-25)+f(25)
y=-700

Je te fais l'équation pour x=10

y=f'(10)(x-10)+f(10)

f(10)=470
f'(10)=147

En remplaçant :

y=147(x-10)+470 doncy=147x-1000

A toi de vérifier l'autre.

mon tableau de variation est-il bon ?

5)tangente au point d'abscisse 25
y=f'(25)(x-25)+f(25)
f(25)= -700
f'(25)=?
En remplaçant :
y=? (x-25)+ 700 donc y=?x-10
pour le f' j'arrive pas je sais plus appliquer

comment as tu fais pour trouver 147 f'(10)pour que je comprennes pour faire l'équation 25 car je suppose quelle était fausse

f'(x)=-3x²+60x-153

f'(10)=-3(100)+60(10)-153=147

donc j'ai corriger est j'ai trouver ceux ci
5)tangente au point d'abscisse 25
y=f'(25)(x-25)+f(25)
f(25)= -700
f'(25)=-1272
En remplaçant :
y=-1272 (x-25)+ 700 donc y=-1272x-2500

f'(25) est faux

apres rectification je crois que ceux se dois etre cel
f'(25)=-3(625)+60(25)-153
f'(25)=-1875+1500-153
f'(25)= -375-153
f'(25)=222
En remplaçant :
y=22 (x-25)+ 700 donc y=222x-2500

Comment comptes-tu ?

-375-153 ne vaut pas 222

pourquoi 183 c'est pas 153

oui , faute de frappe .

-375-153 ne vaut pas 222

Si tu pers 375 et si tu perds 153 , tu crois que tu as gagné 222 ?

non j'ai en est perdu -
f'(25)=-222
En remplaçant :
y=-222 (x-25)+ 700 donc y=-222x-2500
mais excuse moi - et - sa donne + non autrement je comprend rien

Je finis par te donner la réponse.

-375-153=-528

donc je reprend
5)tangente au point d'abscisse 25
y=f'(25)(x-25)+f(25)
f(25)= -700
f'(25)=-3(625)+60(25)-153
f'(25)=-1875+1500-153
f'(25)= -375-153
f'(25)= -528
En remplaçant :
y=-528 (x-25)+ 700 donc y= -528x-2500

f(25)=-700

y=-528(x-25)-700

La réponse est y=-528x+12500

Je te conseille de revoir les calculs algébriques avec des nombres positifs , négatifs , car tu fais des erreurs.
Un jour de Bac , ça ne pardonne pas...

merci de ton aide il me reste plus qu'a tracer la courbe de la fonction f ainsi que les 2 tangentes