DM, géométrie.

Bonjours, j'aimerai de l'aide svp.

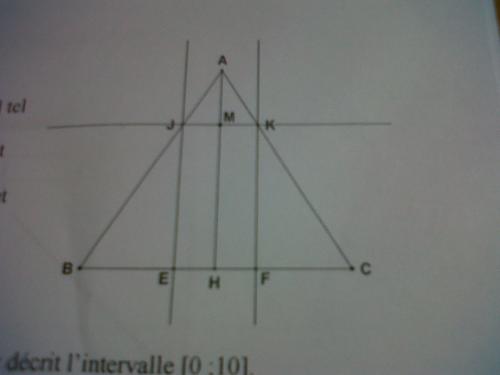
ABC est un triangle rectangle isocèle en A, de hauteur [AH] tel que BC=12cm et AH=10cm.
M est un point de [AH]. La parallèle à (BC) passant par M coupe [AB] en J et [AC] en K.
E et F sont les projetés orthogonaux respectifs de J et K sur la droite (BC).
On pose AM=x

Démontrer que MJ=3/5x
on appelle f(x) l'aire du triangle rectangle JKFE lorsque x décrit l'intervalle [0;10]
a) Montrer que f(x)=12x-6/5x² et vérifier que f(x)=30-6/5(x-5)²

$fichier math$

aidez moi, je n'arrive pas à comprendre :frowning2: , Merci.

Bonjour,
Pour la question 1), tu as des parallèles : tu peux donc penser au théorème de Thalès.

les droites HA et BA sont sécantes en A
J est un point de BA
M est un point de HA
Les doites JM et BH sont parallèles
au triangle JAM et BAH applique le théorème de Thalès connaissant AH et BC

Bis repetita placent

Oui mais ça ne peut pas être ça puisque pour utiliser le théorème de Thalès, il faut que les points soient alignés et qu'ils se coupent en un point. Or la JAM ne se coupe en aucun point et n'est pas alignés.

Des difficultés ne proviendraient-elles pas du mauvais usage du vocabulaire ?
C'est quoi des "points qui se coupent" . Que signifie la phrase "la JAM ne se coupe en aucun point" ?

Dessine uniquement une partie de la figure : juste le triangle ABH, les points J et M, la droite (JM).
Ne dessine pas le côté de la figure situé à droite (Point C,...).
Ne dessine pas (JE).
Tu devrais voir apparaître une configuration connue pour le théorème de Thalès.

$fichier math$

Ah oui, ok! Mais alors moi ça me donne : AJ÷AB=AM÷AH=JM÷BH
C'est dont ça?

Oui, mais le premier quotient ne te servira pas.
Garde AM/AH = MJ/BH
Tu connais les longueurs AH et BH, et tu remplaces AM par x.
Ainsi tu peux exprimer MJ en fonction de x (produits en croix).

Sayé j'ai trouvé! Merci beaucoup.

Et pour la question 2 ?

Eh bien pour la question 2, j'ai fait :
a) f(x)=(6/5x)X(10-x)
=60/5x-6/5x²
=12x-6/5x²

b) 30-(6/5)(x-5)²
=30-(6/5)(x²-10x+25)
=30-(6/5x²-60/5x+6X25/5)
=30-(6/5x²-12x+30)
=30-6/5x²+12-30
=12x-6/5x²

C'est juste.