Tangente et rayon laser !

Hello, je n'arrive pas cet exo , j'aimerai trouver de l'aide. S 'il vous plait.

Sur l'écran d'un jeu vidéo, on voit des avions qui descendent de gauche à droite en suivant la trajectoire indiquée et tirent un rayon laser selon la tangente à leur trajectoire en direction des cibles placées sur l'axe (Ox) aux abscisses numérotées de 1 à 8.
On sait que la trajectoire de l'avion a pour équation :
Y=2+(2/x)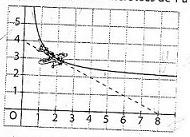

avion

L'avion va-t-il toucher une cible au moment ou il sera au point de coordonné (2;3) ?

2)Determiner l'abscisse de l'avion permettant d'atteindre la cible n°2 ?

Bonsoir,

Pistes,

$y=f(x)=2+2xy=f(x)=2+\frac{2}{x}$

Tu cherches l'équation de la tangente (T) à la trajectoire au point (2,3)

Cette équation sécrit : $y = f^{'} (2) (x - 2) + f (2)$

Tu sais déjà que f(2)=3

Il faut que tu calcules f'(x) puis f'(2) et que tu remplaces dans l'équation de (T)

Ensuite , tu chercheras l'intersection de (T) avec l'axe des abscisses.

Merci bien, j'ai reussit la question a, mais pour la "b" je galere vraiment. J'ai fais une simulation sur geogebra, je pense quil faut trouver une autre tangente qui passe par la 2eme cible. Je trouve une tangente qui passe par (2;0) et (0;7.5) mais je sais pas comment le prouver par le calcul et quelle est l'equation de cette tangente. je sais pas comment trouver la position de l'avion ... Help me please

Indique exactement ce que tu appelles ladeuxième cible : c'est le point de coordonnées (2.0) ?

Idée :

Pour a > 0 , tu cherches l'équation de la tangente (T) au point de la courbe d'abscisse a

y=f'(a)(x-a)+f(a)

S'il faut que (T) touche l'axe des abscisses au point (2,0) , dans cette équation de (T) , tu remplaces x par 2 et y par 0

Tu obtiendras une équation d'inconnue a à résoudre.

comment peut on resoudre
y=f'(a)(x-a)+f(a)
donc f'(a)*(2-a)+f(a)=0 la j'arrive pas trop

Il faut commencer par remplacer f(a) et f'(a) par leurs expressions.

comment on trouve f(a) et f'(a).. ?

$f(x)=2+2xf(x)=2+\frac{2}{x}$

donc :

$f(a)=2+2af(a)=2+\frac{2}{a}$

après calculs ,

$f′(x)=−2x2f'(x)=\frac{-2}{x^2}$

donc

$f′(a)=−2a2f'(a)=\frac{-2}{a^2}$

j'y arrive vraiment pas, je doit le rendre pour demain aider moi s'il vous plait . je sais meme plus ce que je cherche

Je trouve a= racine carré de 2 mais apres je sais pas quoi faire

Revois ton calcul.

Pour l'équation de la tangente en un point d'abscisse a :

$y=(−2a2)(x−a)+(2+2a)y=(\frac{-2}{a^2})(x-a)+(2+\frac{2}{a})$

(T) passe par le point (2,0) si et seulement si :

$0=(−2a2)(2−a)+(2+2a)0=(\frac{-2}{a^2})(2-a)+(2+\frac{2}{a})$

En transformant , en réduisant au même dénominateur a² , tu dois trouver :

$−2(2−a)+2a2+2aa2=0\frac{-2(2-a)+2a^2+2a}{a^2}=0$

donc : $2(2-a)+2a^2+2a =0$

Tu simplifies pour avoir une équation du second degré que tu résous.

Sauf erreur : deux solutions √3-1 , -√3-1

Vu que l'abscisse a cherchée du point de la trajectoire doit être positive , ne conserve que celle qui convient .