Dérivée d'une fonction polynôme
-
AAyans dernière édition par
Bonjour,
f une fonction définie sur R par f(x) = [x^2(-2x^4+15x^2-24)](12)
1\ montrer que f'(x) = -x^5+5x^3-4x
2\ factoriser f'(x) en un produit de fontions polynomes de degre 1
-
Mmathtous dernière édition par
Bonjour,
Commence par montrer comment tu calcules la dérivée.
-
AAyans dernière édition par
je l'ai faite, puis? c la 2eme question que je pige pas
-
Mmathtous dernière édition par
f'(x) = −x5-x^5−x5 + 5x35x^35x3 - 4x
Tu peux déjà mettre x en facteur.
Ou mieux : -x en facteur.
Ensuite, observe le second facteur : tu peux y poser x² = y ce qui te permettra de le factoriser.
-
AAyans dernière édition par
je trouve sa (-x)(x²-1)(x²-4)
-
Mmathtous dernière édition par
ça, pas sa.
Parfait, mais ce n'est pas terminé : x²-1 peut se factoriser en utilisant une identité remarquable (a²-b² =...), ainsi que x² -4.
-
AAyans dernière édition par
(x-1)²
(x-(+2))²
-
Mmathtous dernière édition par
Aïe !
Tu confonds a² - b² avec (a-b)² !
Revois ces formules et retiens-les.
Elles se trouvent partout : dans tes cours, sur internet, ...
-
AAyans dernière édition par
(-x)(x-1)(x+1)(x-2)(x+2) c'est sa ?

-
mtschoon dernière édition par

Bonsoir,
Je regarde ta factorisation , en attendant que Mathtous soit là :
ta dernière réponse est bonne.
-
AAyans dernière édition par
l'énoncé complète
f une fonction définie sur R par f(x) = [x^2(-2x^4+15x^2-24)](12)
1/ montrer que f'(x) = -x^5+5x^3-4x
2/ factoriser f'(x) en un produit de fontions polynomes de degre 1
3/ Etudier les variations de f et dresser son tableau de variation
4/ Quel est le mini de f sur l'intervalle [-3,3]
5/ Quel est le maxi de f sur l'intervalle [-3,3]
6/ Déterminer les coordonées des points d'intersection de C avec l'axe des abcisseJe fais le tableau puis je le met ici par contre pour le 4 et 5 je t rouve pas ^^
-
AAyans dernière édition par
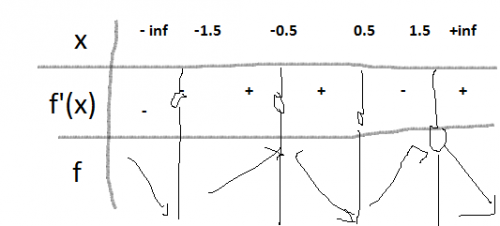
Voila
-
mtschoon dernière édition par

En attendant que Mathtous soit là , je regarde ton tableau de variations .
Que sont ces valeurs -1.5 , -0.5 , 0.5 , 1.5 ? ? ?
Pour trouver le signe de f'(x) utilise la factorisation (-x)(x-1)(x+1)(x-2)(x+2)
-
Mmathtous dernière édition par
Ton tableau devrait contenir (en première ligne) les valeurs d'annulation des facteurs de f '(x) : 0, 1, -1, 2, -2 ( à placer dans le bon ordre ...).
-
Mmajortom dernière édition par
Bonjour,
j’essaie de solutionner le même exercice mais je m'interroge dés le 1/;On trouve f`(x)= 12( -x^5+5x^3-4x)
Je ne trouve pas la règle qui permet d'éliminer le facteur (12)...
Merci
-
Mmathtous dernière édition par
Bonjour majortom.
Regarde, il y a une division par 12 dans l'énoncé.
-
Mmajortom dernière édition par
Bonjour mathtous.
Oui bien sur, en fait le probleme vient que j'avais développé le numérateur de la fonction par x^2 en oubliant que la dérivée des produits n'est pas égale au produit des dérivées.
En appliquant (uv)= uv + uv` il n'y a plus de problème.Par contre je patauge sur le 2/
J'appelle à l'aide si je galère de trop.Merci
-
Mmathtous dernière édition par
Cherche des racines "évidentes".
-
Mmajortom dernière édition par
OK,
En reprenant la méthode ci dessus.
je pose x^2=y et donc........y^2-5y+4 et j'imagine que les racines "évidentes" passent par
1 -5 +4=0 : y=1 qui est racine.........Finalement
(-x)(x-1)(x+1)(x-2)(x+2)Ok c'est nouveaux et intéressant.
Je me colle bientôt à la suite......
Merci
-
Mmathtous dernière édition par
Bon courage.
-
Mmajortom dernière édition par
Merci pour tes encouragements mathtous.
3/ Étudier les variations de f et dresser son tableau de variation
le probleme c'est que j'arrive à ce résultat uniquement grâce à la lecture du graphe ci dessous
de fait je n'ai aucune idée de la manière d'étudier le signe d'une dérivée avec autant de valeurs de x qui l'annulent.....
Je ne vois pas comment utiliser le théorème du signe de a à l’extérieur des solutions, etc...il va aussi falloir que j'apprenne à utiliser les balises

-
Mmathtous dernière édition par
Avant tout, peux-tu me détailler le calcul de f(1) (ou de f(-1) qui est la même chose) ?
-
Mmajortom dernière édition par
Alors,
f(-1)=[-1^2(-1*(-1)^4+15*(-1)^2-24]/12
=1(-1+15-24)/12
=-10/12
=-5/6ce qui donne la même chose pour f(1) et une histoire semblable pour f(-2) et f(2)!?
-
Mmajortom dernière édition par
j'ai arrangé un peu le 1er post du jour, il était illisible
-
Mmathtous dernière édition par
Non : c'est (-1)² et pas -(1)²
De plus, je ne comprends pas :
Citation
-1*(-1)^4que fait le -1 devant ?
Calcule f(1) au lieu de f(-1) : tu éviteras peut-être des fautes de signes.
-
Mmajortom dernière édition par
Hum!
f(1)=[1(-21^4+151^2-24)]/12
=-11/12
:rolling_eyes:
-
Mmathtous dernière édition par
Bon.
Passons à la suite :
ton histoire de signe de a à l'extérieur des racines fonctionne uniquement pour un polynôme de degré 2, et ici la dérivée est de degré 5.
Mais qu'importe : tu utilises un tableau des signes puisque tu connais la factorisation de f '(x).
Simplement, tu auras plein de lignes avant d'avoir son signe final.
-
Mmajortom dernière édition par
Mais si mais c'est bien sur!
ça me reviens.
Merci.
-
Mmathtous dernière édition par
De rien.
N'hésite pas si tu as d'autres questions.
-
Mmajortom dernière édition par
Je reprendrais ce fil plus tard et en ouvrir un autre plus urgent....
A bientôt.
-
Mmathtous dernière édition par
A+