Série statistique

Bonjour a tous, j'ai un gros problème sur exercice, pouvez-vous m'aider s'il vous plaît.
Voici sujet: Une série statistique est représentée par le diagramme en bâtons ci-dessous.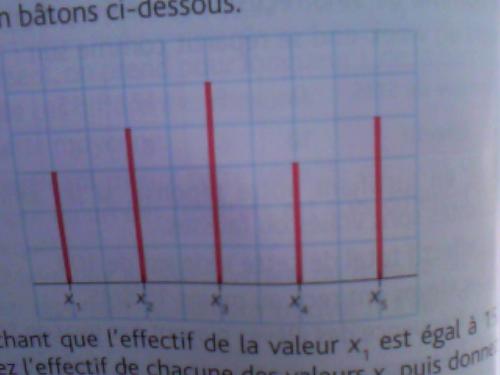

$fichier math$
[b*]a)*[/b] Sachant que l'effectif de la valeur x1, est égal à 15, donnez l'effectif de chacune des valeurs x1, puis donnez l'effectif total.

b) Sachant que l'effectif total est de 266 individus, déterminer la fréquence et l'effectif de chacune des valeurs x1.
Ou j'en suis :
Je n'arrive ^pas du tout à la 1ere question, en faite je ne la comprends pas

Aider moi s'il vous plait
Merci d'avance

Bonjour momo30,

Pour les deux questions, tu utilises la proportionnalité.

a)
x1 correspond à 3 carreaux et x1 = 15
x2 correspond à 4 carreaux donc x2 = ...
etc ...

l'effectif total ... c'est alors facile.

b)
La somme des carreaux vaut 266

soit u la valeur d'un carreau.

3u + 4u + 5u + 3u + 4u = 266

donc u = ... (valeur d'un carreau)

Tu en déduis les valeurs des xi :

X1 correspond à 3 carreaux donc x1 = 3u = ...

Iron
Bonjour momo30,

Pour les deux questions, tu utilises la proportionnalité.

a)
x1 correspond à 3 carreaux et x1 = 15
x2 correspond à 4 carreaux donc x2 = ...
etc ...

l'effectif total ... c'est alors facile.

b)
La somme des carreaux vaut 266

soit u la valeur d'un carreau.

3u + 4u + 5u + 3u + 4u = 266

donc u = ... (valeur d'un carreau)

Tu en déduis les valeurs des xi :

X1 correspond à 3 carreaux donc x1 = 3u = ...

pour la b) u=14 c ça??

Oui, 1 carreau représente 14 unités

X1 correspond à 3 carreaux donc x1 = 3u = 3×14=42 donc c faux, hein ??

C'est correct.

D'après ton énoncé, les deux questions a) et b) ne peuvent être que complètement indépendantes.

Combien as-tu trouver pour effectif total pour la question a) ?

Iron
C'est correct.

D'après ton énoncé, les deux questions a) et b) ne peuvent être que complètement indépendantes.

Combien as-tu trouver pour effectif total pour la question a) ?
95, pourquoi?

Iron
C'est correct.

D'après ton énoncé, les deux questions a) et b) ne peuvent être que complètement indépendantes.

Combien as-tu trouver pour effectif total pour la question a) ?
95, pourquoi?

Tu es en quelle classe ?

a) C'est correct

Les deux séries a) et b) sont représentées par le même diagramme en bâton mais n'ont pas les mêmes effectifs.

Il ne faut pas t'étonner si tu obtiens :
effectif de x1 : n1 = 15 pour a)
et n1 = 42 pour b)

Etant représentées par le même diagramme en bâton, chaque valeur $x_i$ des deux séries a) et b) ont la même fréquence $f_i$

Tu peux t'appuyer sur cela pour calculer les fréquences de la question b)

Sinon, tu calcules tous les effectifs n1, n2 ... n5 des valeurs x1, x2 ... x5 puis tu calcules leurs fréquences respectives.

$fi=niNf_{i}=\frac{n_{i}}{N}$
avec
ni : effectif de la valeur xi
N : effectif total

Je dois quitter, j'espère que tu t'en sortiras maintenant ...
Bonne soirée