Le Cercle d'Euler !

Voilà, je suis en seconde et je dois rendre un dm à la rentrée il y a un exercice que je n'ai pas compris, pourrait-on m'aider ?

Voici le problème que je n'arrive pas à résoudre :

a)Tracer un triangle ABC quelconque de grande taille. Tracer les 3 hauteurs et l'orthocentre H. Placer les points D,E,F,G milieux respectifs de (AB), (AC), (HC), (HB) c'est entre crochets mais je ne sais pas comment les faire sur mon clavier qwerty. Donc j'ai déjà fait tout ça, j'ai construit entre autre la figure.
Je bloque sur cette question : montrer que DEFG est un rectangle si quelqu'un pouvait me donner des pistes et m'aider à resoudre cette question ce serait top ! :).

b) Placer les points I,J milieux respectifs de (AH), (BC)
montrer que DIFJ est un rectangle. Question du même type que je n'arrive pas à demontrer

c/ montrer que les segments (DF), (EG) et (IJ) ont le même milieu et la même longueur
d/monter que les 6 milieux appartiennent à un même cercle.
e) montrer que les 3 pieds des 3 hauteurs du triangle ABC appartiennent aussi à ce cercle.

Je ne me suis pas attardée sur ces 3 autres questions que j'espère démontrer après le petit a) et b).

merci de votre compréhension, j'attends au plus vite que vous m'éclairiez

Bonsoir

a) Pour montrer que DEFG est rectangle, il suffit d'utiliser le théorème des milieux dans ABC d'une part et dans CAH d'autre part pour prouver que (DE) et (EF) sont perpendiculaires (même raisonnements pour deux autres angles droits).

D'accord, mais comment je fais pour prouver que les angles sont droits ?

mais pour prouver que ED=FG je peux dire que comme les deux sont égaux à la moitié de (BC) alors ils sont égaux ? Ou je suis obligée de prouver que (EF) // (DG) ?

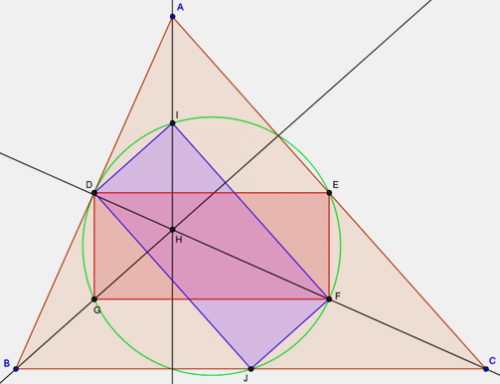
$fichier math$

Je te montre les arguments pour (DE) perpendiculaire à (EF).

Dans ABC d'après le théorème des milieux, (DE) est parallèle à (BC) puisque D et E sont les milieux de [AB] et [AC].

De même dans ACH, d'après le théorème des milieux, (EF) est parallèle à (AH) puisque E et F sont les milieux de [AC] et [CH].

Or, (BC) et (AH) sont perpendiculaires, puisque AH est la hauteur issue de A dans ABC.

Donc ...