lectures graphiques : dérivée

[stylo50]

Bonjour , voici mon DM

On considère une fonction f définie et dérivable sur l'intervalle [ -2 ; 4 ] . On note f' la fonction dérivée de f . La courbe Cf tracée ci-dessous représente la fonction f et T la tangente en B à Cf .

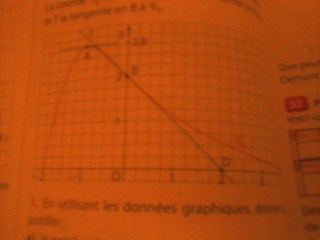
1- En utilisant les données graphiques , donner sans justifier :

a) le nombre de solutions de l'équation f(x) = 1 et un encadrement d'amplitude 0,25 des solutions éventuelles ;

b) la valeur de f ' (-1) .

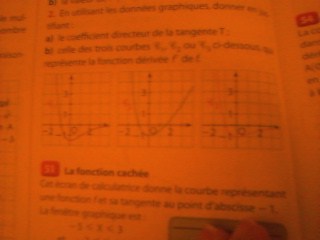
2- En utilisant les données graphiques , donner en justifiant :

a) le coefficient directeur de la tangente T ;

b) celle des trois courbes C1 , C2 , C3 ci-dessous , qui représente la fonction dérivée f ' de f .

voici mes réponses :

a) pour l'équation f(x) = 1 il y a 2 solutions : -1.7 et 1.2
b) pour f'(-1) j'ai trouvé 2.8 mais je ne suis pas sure

merci pour tous ceux qui m'aideront

[Noemi]

Bonsoir stylo50,

Pour 1 a) il est demandé un encadrement de la solution.
b) pour x = -1 la tangente est ...... donc f'(-1) = ....
2 a) Choisis deux points de la tangente est calcule le coefficient directeur.
b) analyse les variations de la fonction donc le signe de la dérivée.

[stylo50]

pour la 2) a- j'ai trouvé le coefficient directeur de T qui est -1
pour la 2) b- j'ai trouvé que c'est la courbe 3 qui représente la dérivée de
f ' de f

pour la 1) a et b je bloque

[Noemi]

Les scans sont difficiles à lire
2 a) juste,
2 b) les courbes sont difficiles à lire.

1 a) donne un encadrement
à la place de 1,2 cela donne par exemple 1,05 ; 1,3

f'(-1) = 0, la tangente est horizontale.

[stylo50]

excusez-moi pour les scans donc pour la 1) a- pour le deuxième encadrement j'ai mis [ -1.6 ; -1.8 ]

[Noemi]

Amplitude 0,25, soit -1,6 ; -1,85

[stylo50]

merci noemi pour votre aide

a+