sangaku des 9 sphères

titre de l'exo : sangaku des 9 sphères

sur un plan on pose une sphère de centre A et de rayon R et on dispose autour de cette sphère huit sphere identiques de rayon r (une ayant pour centre B) tangentes entre elles et tangentes a la grande sphère. On cherche a déterminé le rapport r/R.

a) demontrer que r= PB x sin ∏/8

b) demontrer que : PB²=4rR

c) en deduire la valeur du rapport cherché en fonction de sin ∏/8 et en donner la valeur approchée a $10^{-2}$ près. $fichier math$

j'ai un figure mais j'arrive pas a l'inserer

Bonjour, ( un "Bonjour" fait plaisir )

J'espère que tu as scanné la figure (exclusivement la figure ) et que tu en as fait un fichier-image enregistré sur ton disque dur .

Au dessous du cadre Réponse , tu dois voir en bleu Ajoute une image

Tu cliques dessus et tu suis le mode d'emploi.

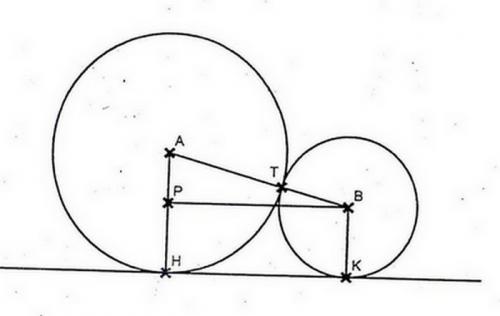
enfin voila ma figure dsl merci pour l'explication

Pour traiter la première question , il faut que tu penses à une autre vue des sphères.

Le schéma de ton énoncé est une coupe "verticale" passant par le centre de la grosse sphère et le centre d'une des petites sphères.

Je te suggère une coupe "horizontale" passant par tous les centres des petites sphères.
Tu pourras utiliser la définition du sinus de l'angle $\text{\widehat{bpc}$ dans le triangle PBC rectangle en C pour répondre à la question.

$sin⁡bpc^=bcpb\sin\widehat{bpc}=\frac{bc}{pb}$

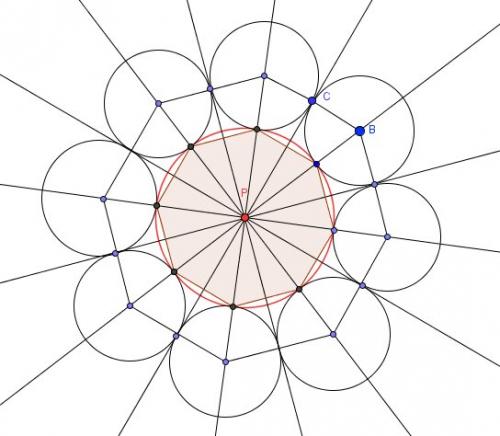
Voici le schéma de la coupe :

$fichier math$

bonjour je n'ai pas trop compris car les points que tu as mis ne correspondent pas a ma figure (et d'ailleurs mercu de d'etre donnr du mal pour la figure ) et je vois comment on peut repondre a la question la premiere surtout !

Je viens de te remettre le schéma avec les notations du schéma de ton énoncé.

La seule difficulté de cet exercice est la vision dans l'espace.

Comme je te l'ai déjà dit , le schéma de ton énoncé est une coupe "verticale" passant par le centre A de la grosse sphère et le centre B d'une des petites sphères.

Avec ce schéma , tu ne peux pas répondre à la première question !

Il faut que tu aies une autre "vue" .

Je t'ai fait une coupe "horizontale" passant par tous les centres des petites sphères.

( coupe par un plan parallèle au plan de base et passant par B ( et par les 7 autres centres des petites sphères )

Le point P et le point B sont ceux de la coupe verticale du schéma de ton énoncé.

Prends le temps nécessaire pour comprendre ce schéma...

Pour le calcul : l'angle au centre de sommet P est divisé en 16 parties égales.

Comme l'angle au centre total vaut 2∏ , chaque partie vaut 2∏/16 c'est à dire ∏/8

Utilise la définition du sinus dans le triangle rectangle PCB