Exercice sur les droites concourrantes
-
Ccedlo dernière édition par
Bonjour a tous, j'ai ce dm et je bloc a certaine question:
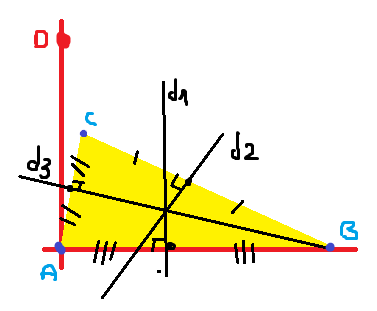
On considère un triangle (non aplati) ABC et un point D tel que (A,B,D) soit un repère orthonormé.
On note (a;b) les coordonnées du point C dans ce repère.
on note d1,d2 et d3 les médiatrices respectives des segments [AB], [BC] et [CA].- pourquoi peut-on affirmer que b est différent de 0 ?
- en utilisant l'équivalente: " M(x;y)appartient a d2 <=> BM² = CM² " montrer qu'une équation de la droite
d2 est:
y= [(1-a)/b ]x + (a²+b²-1)/2b
- déterminer de même une équation de chacune des droites d3 et d1.
- montrer que les droites d1,d2 et d3 son concourantes
- quelle propriété possède le point de concours de ces trois droites ?
Mes réponses:
-
Si b était nul, le triangle ABC serait aplati
-
J'ai réussi a prouver en prenant que A(0,0) que B(1,0) que M(x,y) et C(a,b)
-
je n'arrive pas a faire d1
et pour d3 j'ai trouver y= -ax/b + (a^2 + b^2)/2b est ce correct??
4.IL faut selon moi que f(x), g(x) et h(x) les équations respectives de (d1), (d2) et (d3).
Il faut démontrer que f(x) = g(x) et f(x) = h(x) ont la même solution- Ce point sera a égale distance de A et B et C
J'espère que vous pourrez m'aidez
-
Mmathtous dernière édition par
Bonjour,
La droite d1 est particulière : parallèle au second axe.
Son équation est donc de la forme x = un nombre constant.
Il suffit pour trouver ce nombre d'exprimer que d1 passe par le milieu de [AB]
-
Ccedlo dernière édition par
pour d1 on a f(x)=1/2
c'est la question 4 que je bloque maintenant
-
Mmathtous dernière édition par
Citation
pour d1 on a f(x)=1/2Non: f(x) c'est y. Et ce n'est pas y qui vaut 1/2 mais x.
L'équation de d1 est x = 1/2 (il n'y a pas de y : l'équation ne peut pas se mettre sous la forme y = mx+p).La question 4 devient alors facile : on a déjà la moitié de la réponse : x = 1/2.
Reste à voir si y est le même pour d2 et d3.
-
Ccedlo dernière édition par
Pour voir si y est le meme pour d2 et d3 je résout d2=d3 ?
-
Mmathtous dernière édition par
Tu peux faire cela, mais il y a plus simple : remplace x par 1/2 dans l'équation de d2 : tu trouves y.
Fais de même dans d3 : il suffit de vérifier si on trouve la même valeur pour y ou pas.
-
Ccedlo dernière édition par
Tout d'abord les réponse a la question 3 sont bien:
-
Pour d3 une équation de la droite est y= -ax/b + (a^2 + b^2)/2b ?
-
Pour d1 une équation de la droite est x= 1/2 ?
Ensuite pour la question 4 :
Je dois prendre x= 1/2 et le remplacer dans les equation de d2 et d3 et je doit obtenir le meme résultat ?
-
-
Mmathtous dernière édition par
C'est bien ça.
-
Ccedlo dernière édition par
En remplacant x par 1/2 dans d2 et d3 j'obtient:
-Pour d3 y= -a+ a^2+ b^2 / 2b
-Pour d2 y= -a+ a^2+ b^2 / 2b
Mais je suis pas sur
-
Mmathtous dernière édition par
Tu obtiens bien la même chose, cela prouve que les 3 droites sont concourantes ; leur point commun a pour coordonnées :
(1/2 ; (-a+a²+b²)/2b)Attention à ton dessin : en général d3 ne passe pas par B.
-
Ccedlo dernière édition par
D'accord mais je n'ai pas compris quelle sont les coordonné du point commun
-
Mmathtous dernière édition par
Pour x : 1/2 , et pour y : la valeur commune trouvée, notons-la y0 :
y0 = (-a+a²+b²)/2b il est normal qu'elle dépende de a et de b.Tous les points de d1 ont obligatoirement une abscisse égale à 1/2, et une ordonnée quelconque.
L'intersection de d1 et d2 est le point de coordonnées (1/2 ; y0)
L'intersection de d1 et d3 est le même point.
Donc les 3 droites passent par ce point.
-
Ccedlo dernière édition par
Peut on appeler le point d'intersection des trois droite P par exemple
-
Mmathtous dernière édition par
Si tu veux.
Mais as-tu la réponse à ta précédente question ? Sinon, précise ta demande.
-
Ccedlo dernière édition par
OUi j'ai compris pour prouver quelle sont concourantes merci
et pour la question 5 la réponse que j'ai mise dans l'énoncé est elle correcte ?
-
Mmathtous dernière édition par
C'est juste.
Tu sais aussi que ce point est le centre du cercle circonscrit au triangle.
-
Ccedlo dernière édition par
Merci beaucoup de m'avoir aidé
Bonne fin de journée
-
Mmathtous dernière édition par
Merci et bon courage.