Exercice autour d'une parabole.

Bonjour, j'ai eu cet exercice mais je ne trouve pas la dernière question (texte en gras) , pourriez-vous m'aider? S'il vous plait.

Voici l'énoncé:

Dans un repère, P est la parabole d'équation y=x²
A et B sont deux points distincts d'abscisses a et b, I milieu de [AB].

Faire une figure
Déterminer les coordonnées du point I.
3a) Déterminer les équations des tangentes à P en A et B.
b) Déterminer les coordonnées du point J.
4a) Placer sur la figure le milieu M du segment [IJ].
b) A l'aide d'un logiciel de géométrie dynamique, observer la position du point M. Que peut-on conjecturer? Démontrer cette conjecture.
Tracer la tangente à la parabole P en M.A l'aide du logiciel dynamique, observer les positions relatives des droites (AB) et T. Que peut-on conjecturer? Démontrer cette conjecture.

Merci d'avance !

Bonjour,

Je suppose que J est le point d'intersection des tangentes en A et en B

Tu peux faire une figure dynamique avec GeoGegra.

C'est ce que je viens de faire, mais je t'en donne une image fixe...

Si ça peut t'être utile , la voilà :

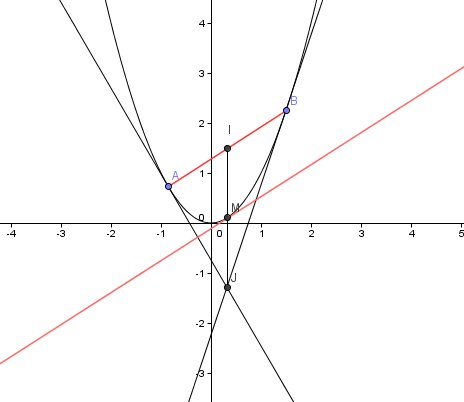
$fichier math$

Oui en effet J est le point d’interception des deux tangentes, j'ai oublié de la préciser.
La figure je l'ai faite aussi mais je n'arrive pas à faire de conjecture et donc pas non plus la démontrer...

Si tu regardes le schéma que je t'ai donné , tu dois bien voir que le tangente en M est parallèle à (AB)
( Couleur
rouge)

Effectivement oui, merci. Je vais réfléchir à la démonstration.

Bon, j'ai eu une idée:
Je pensais calculer le coefficient directeur de la tangente en M puis calculer celui de la droite (AB).
Et après voir si les droites ont le même coefficient directeur , si oui elles sont parallèles je pense.
Le problème c'est que je ne sais pas trop comment m'y prendre. Pourriez vous me donner une piste? S'il vous plait. Merci beaucoup.

Ton idée est la bonne.

D'après ton énoncé , tu as trouvé les coordonnées de I et de J ( en fonction de a et b)

Tu peux donc trouver les coordonnées de M milieu de [IJ]

Tu a démontré précedemment que M appartient à P

Le coefficient directeur de la tangente en Mest $f'(x_m)=2x_m$

**Le coefficient directeur de (AB)**est $yb−yab−a=b2−a2b−a=b+a\frac{y_b-y_a}{b-a}=\frac{b^2-a^2}{b-a}=b+a$

Tu dois trouver que ces deux coefficients directeurs sont égaux.

Bons calculs.

Merci beaucoup pour votre aide !