Pyramide (Base triangle isocèle)

Bonjour
Je suis pas bien en géométrie et j'ai besoin d'explications pour cet exercice s'il vous plaît
Merci d'avance

construire un patron de la pyramide SIJK ci-contre.
Calculer le volume et l'aire totale de cette pyramide.
On donne IS = 6cm; IJ = JK = 5cm.
Les triangles SIJ, SJK, et IJK sont rectangle en J.
Comment faire pour chercher l'aire de IJK
j'ai fait
Aire(IJK) = (5 x 5) / 2 = 12,5
Aire (IJK) = 12,5 cm

V = (Aire de la base x H) / 3
Calculons SJ
SIJ est rectangle en J
D'après le théorème de Pythagore
IS² = IJ² + SJ²
SJ² = IS² - IJ²
SJ² = 6² - 5²
SJ² = 36 - 25
SJ² = 11
SJ = √11

Ske j'ai bon jusque là?

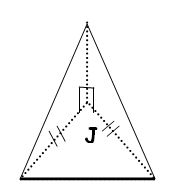
Pyramide à base triangle isocèle

J'ai repris la figure pour plus d'information
j'ai besoin de votre aide s'il vous plaît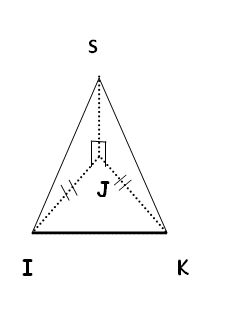

pyramide(Base triangle isocèle)

Salut
Oui, tu as bon jusqu'ici, mais tu as laissé de côté la question du patron...
Quelle(s) question(s) te poses-tu ?

Bonjour

Voilà j'ai trouvé
Aire(IJK) = 12,5 cm²
Hauteur SJ = √11
V= (12,5√11) / 3
Ce que je voudrais c'est: "est ce que je dois laisser comme ça le résultat?"
Merci de vos réponses

Pour la question1)
Je voudrais aussi que l'on m'explique comment on fait le patron? quels sont les différentes étapes à suivre?
merci

oui, ça peut rester comme ça si l'énoncé ne demande pas de valeur approchée

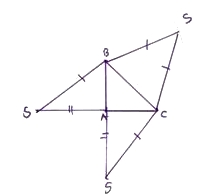
pour le patron, imagine la pyramide posée sur sa base IJK puis déplie les trois autres faces sur le m^me plan comme s'il y avait des charnières comme ceci : $fichier math$

Merci Zauctore, donc les cotés des triangles de la surface latérale doivent être égaux aux cotés du triangle à la base.

Merci Zaucore, j'ai compris

Re-bonjour Zauctore
Voici le patron de la pyramide
est ce que c'est bon?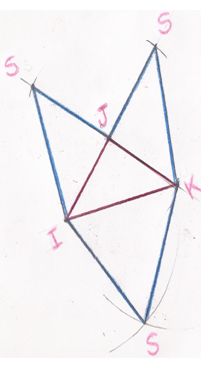

Patron d'un tétraèdre

Re.

Je n'arrive pas trop à détecter si tu as bien reporté les "bonnes" longueurs (tu n'as indiqué aucun codage).

Les deux segments [IS] sur ta figure doivent être égaux, les deux [SK] aussi bien entendu - et leurs quatre longueurs sont aussi égales.

Concernant l'aire latérale, tu n'as pas encore calculé l'aire de IKS : le patron est là pour t'aider à le faire !

Attention : ce que tu as écrit ci-dessus à 10:08 ne me semble pas correct.

Merci Zauctore pour ces remarques, elles m'ont beaucoup servies j'ai repris ma figure.
Calculons IK dans le triangle IJK
IJK est un triangle rectangle en J.
D'après le théorème de Pythagore on a:
IK² = IJ² + JK²
IK² = 5² + 5²
IK² = 50
IK = 5√2
Pour calculer l'aire de IKS, je place un point H milieu de [IK] et je calcule la hauteur [SH] du triangle IKS
On a: SI = 6 cm
IH = 1/2 IK
IH = (5√2) / 2

SIH est un triangle rectangle en H.
D'après le théorème de Pythagore on a:
SI² = IH² + SH²
SH² = SI² - IH²
SH² = 6² - ((5√2) / 2)²
J'ai un problème pour la suite?????

Bonjour

Pour calculer ((5√2) / 2)², en revenant à la définition
écris que c'est (5√2 / 2) × (5√2 / 2).

Je vous présente toutes mes excuses j'ai des problèmes de connections...
je termine tout à l'heure avec votre compréhension s'il vous plaît

Ne t'excuse pas, je ne suis pas souvent en ligne non plus !

Merci à Zauctore et Noemi pour vos explications, cela m'a beaucoup aidé en classe, car je ne comprenais rien à cette
Merci Infiniment

......A cette leçon