Les inéquations Casse-tête pour moi
-
Sserenade dernière édition par
Bonjour
J'ai de sérieuses difficultés avec les inéquations, y'en a que je comprenais mais d'autres je sais pas les faire, et j'ai besoin de vos explications s'il vous plaît.Voici quelques unes que j'ai trouvé sur le net et que je voudrais résoudre
- (1+x)²(5-x) / 1-2x > 0
- (x²+1)(x-2) / (2-x)(3-2x) ≤ 0
- 4 / (x-1)² ≥ 1
- x³ ≤ x²
Mes réponses
1.x -oo -1 1/2 5 +oo
(1+x)² + 0 + + +
5-x + + + 0 -
1-2x + + 0 - -
Q + 0 + 0 - 0 +
1/2 est une valeur interdite
Donc S= ]-oo;-1[ ∪]-1;1/2[ ∪]5;+oo[
-
IIron dernière édition par
Bonjour serenade,
Ton résultat est correct.
-
Sserenade dernière édition par
x -oo -1 1 2 3/2 -oo
x²+1 + 0 + 0 + + +
x-2 - - - 0 + +
2-x + + + 0 - -
3-2x + + + + 0 -
Q - 0 - 0 - 0 - 0 +
Valeur interdite 2 et 3/2
S= ]-oo;-1] ∪[-1;1] ∪[1;2[ ∪]2;3/2[
-
Sserenade dernière édition par
bonjour Iron
-
IIron dernière édition par
- (x²+1)(x-2) / (2-x)(3-2x) ≤ 0
Pour la seconde, pense à simplifier ...
-
Sserenade dernière édition par
je simplifie comme ça
(x²+1)(x-2) / (2-x)(3-2x) ≤ 0
. (x²+1)(2-x) / (2-x)(3-2x) ≤ 0
x²+1 / 3-2x ≤ 0
C'est bien ça?
-
Sserenade dernière édition par
Donc après simplification
x -oo -1 1 3/2 -oo
x²+1 + 0 + 0 + +
3-2x + + + 0 -
Q + 0 + 0 + 0 -
Valeur interdite 3/2
S=]3/2;+oo[
-
IIron dernière édition par
Une erreur de signe
Au numérateur tu as (x-2) et au dénominateur (2-x)
Pour faire apparaître (x-2) au dénominateur (par ex) pour pouvoir simplifier.
il faut donc changer le signe du dénominateur
(2-x)(3-2x) = -(x-2)(3-2x) = (x-2)(2x-3)
-
Sserenade dernière édition par
Ah d'accord merci
(x²+1)(x-2) / (x-2)(2x-3) = (x²+1) (2x-3)
x -oo -1 1 3/2 +oo
x²+1 + 0 + 0 + +
2x-3 - - - 0 +
Q - 0 - 0 - 0 +
Valeur interdite 3/2
S= ]-oo;-1] ∪[-1;1]∪[1;3/2[
-
IIron dernière édition par
Est-tu sûre que -1 et 1 annule (x²+1) ?
-
Sserenade dernière édition par
C'est là où je ne comprends pas quand il y'a des x², je me perds... voulez vous m'expliquer ce qu'il faut faire dans ces cas là???
-
IIron dernière édition par
Tu connais les fonctions de référence (appelées aussi fonctions usuelles)
Tu sais donc que pour tout x réel x²≥0
x² ≥ 0
x²+1 ≥ 0+1
x²+1 ≥ 1Or 1 > 0
soit x²+1 ≥ 1 > 0
ce qui te donne x²+1 > 0
x²+1 est toujours strictement positif, cette expression ne s'annule pas
Pour résoudre ton inéquation
(x²+1) / (2x-3) ≤ 0
Tu connais déjà le signe du numérateur (et tu sais qu'il ne s'annule pas)
L'expression sera du signe du dénominateur ce qui te simplifie la vie ...Me dire si je n'ai pas été suffisamment clair.
-
Sserenade dernière édition par
Merci pour ces explications
Pouvez vous me faire un tableau s'il vous plaît où si vous le voulez bien j'en fais un et vous me le corrigez....
-
IIron dernière édition par
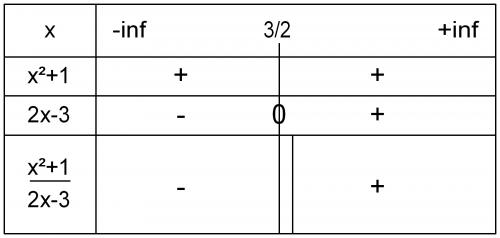
-
Sserenade dernière édition par
Merci je reviendrai pour le reste
-
IIron dernière édition par
Ok
Pour les inéquations 3) et 4) il faut amener un des membres à 0 puis mettre éventuellement au même dénominateur si nécessaire.
A < B ⇔ A-B < 0
-
Sserenade dernière édition par
Merci
Pour l'inéquation 3) voilà ce que j'ai fait4/(x-1)² ≥ 1
4/(x-1)² - 1 ≥ 0
4 - (x-1)² / (x-1)² ≥ 0
[ 2 + (x-1)][ 2 - (x-1)] / (x-1)² ≥ 0
(x+1)(-x +3) / (x-1)² ≥ 0x -inf -1 1 3 +inf
x+1 - 0 + + +
-x+3 + + + 0 -
(x-1)² + + 0 + +
Q - 0 + 0 + 0 -
Valeur interdite 1
S = [-1;1[ ∪ ]1;3]
-
IIron dernière édition par
Ta solution est correcte.
Par contre, dans ton tableau ligne Q, il faut une double barre en 1 et non pas 0
Tu t'en sors plutôt bien !
-
Sserenade dernière édition par
Bonjour Iron
Pour x³ ≤ x² ou x³ - x² ≤ 0
Je factorisex²(x-1) ≤ 0
x² = 0x-1 = 0
x =1x -oo 0 1 +oo
x² + 0 + +
x-1 - - 0 +
x²(x-1) - 0 - 0 +
-
IIron dernière édition par
Bonjour serenade,
C'est juste. Quel est donc ton ensemble de solution ?
-
Sserenade dernière édition par
Voici l'ensemble des solutions
S=]-oo;0] ∪[0;1]
-
IIron dernière édition par
x²(x-1)
≤0L'inégalité est au sens large (ce n'est pas <) ... donc ?
-
IIron dernière édition par
serenade
Voici l'ensemble des solutions
S=]-oo;0
]∪
[0;1]Tu as pris le "0" avec raison donc S = ...
-
Sserenade dernière édition par
Citation
L'inégalité est au sens large (ce n'est pas <) ... donc ?
Tu as pris le "0" avec raison donc S = ...
Je comprends pas ce que vous voulez dire s'il vous plaît
-
IIron dernière édition par
serenade
Voici l'ensemble des solutions
S=]-oo;0
]∪
[0;1]Tu inclus "0" dans les deux intervalles donc S = ]-∞;1] en fait, ok ?
si tu te réfères à ton tableau de signe, l'inégalité x²(x-1) ≤ 0 étant au sens large, la valeur "0" peut être atteinte, x=0 fait partie des solutions, ce n'est pas une valeur à exclure, d'où :
S = ]-∞;1]
-
Sserenade dernière édition par
Merci je comprends maintenant
Je poste le restant des exercices demain, j'ai cour aujourd'hui.
Bonne journée à tous
-
Sserenade dernière édition par
Bonjour
j'ai fait mes autres exos
Voici mes solutions pour ceux ce que j'ai compris, vous corrigez pour moi-
2x+3/x+4 ≥ 3
-
4-x/8-x ≤ 1-3x/2+x
-
(3-x)(2+x)(1-x) < 0
-
25-x²/3x+2 ≤ 0
-
1/x ≤ x
-
1/x ≥ x³
-
x² > 1/x
Mes résultats sont
-
S = [-9;4[
-
S = [0;-2[ ∪ [4/27;8[
-
S = ]-oo;-2[ ∪ ]1;3[
-
S = [-5;-2/3[ ∪ [5;+oo[
mais pour le reste j'ai des difficultés
Merci de votre compréhension
-
-
IIron dernière édition par
Bonjour Serenade,
Je n'aurai pas de dispo avant mi-semaine prochaine probablement.
Si tu souhaites de l'aide rapidement, je te suggère de créer un nouveau poste.
désolé de ne pour voir t'aider ce week-end ...
-
Sserenade dernière édition par
D'accord Iron
demain je posterai un nouveau sujet