Déterminer les extremums d'une fonction quotient à l'aide des dérivées

Bonsoir à tous,
voilà mon problème:

je n'arrive pas à résoudre cette exercice car je n'arrive pas à comprendre la leçon sur les dérivées. Ne croyez pas que je suis fainéant mais je demande votre aide pour résoudre ce problème et avant tout j'aimerais avoir des explications sur la leçon et sur les solutions car mon gros problème est que je n'arrive pas à comprendre mes leçons en maths et à résoudre les exos!

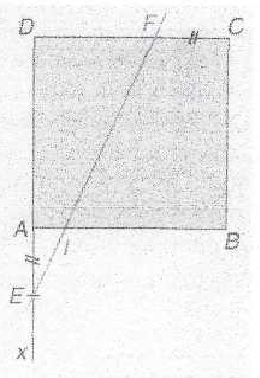
ABCD est un carré de côté 1.

Les points E et F appartiennent respectivement à la demi droite [Ax) et au segment [DC] et vérifient AE = CF.

I est le point d"intersection des droites (AB) et (EF).

On pose AE = x.

1° a) Démontrer que
AI= $x−x2x+1\frac{x-x^{2}}{x+1}$

b) Déterminer la position du point E pour que la distance AI soit maximale.
2° Quelle est la position du point E qui rend l'aire du triangle AIE maximale?

*merci *

figure du problème

Bonsoir,

Piste pour démarrer,

Avec le théorème de Thalès :

$eaed=aidf\frac{ea}{ed}=\frac{ai}{df}$

DE=DA+AE=1+x
DF=DC-CF=1-x

Tu remplaces dans l'égalité des rapports , tu fais les produits en croix et tu en déduis l'expression de AI

J AI PAS COMPRIS MONTRE MOI UN EXEMPLE

Bonjour,

Il n'y a pas d'exemple à donner ... mtschoon te donne une piste : utiliser Thales qui te permet de calculer AI en fonction des données

Citation
Tu remplaces dans l'égalité des rapports , tu fais les produits en croix et tu en déduis l'expression de AI

je ne comprend pas cette phrase

Je détaille un peu .

En remplaçant AE , DE et DF par leurs valeurs :

$x1+x=ai1−x\frac{x}{1+x}=\frac{ai}{1-x}$

Produits en croix :

$a i (1 + x) = x (1 - x)$

Termine pour obtenir AI

AI= $ai=x-x^{2}-1-x=1-x$
C EST BON?

NON !

$ai=x(1−x)1+xai=\frac{x(1-x)}{1+x}$

ah oui! désolé je fais comment maintenat je ne trouve pas comment continuer?

C EST POUR pressé mais je dois le rendre demain
svp!

Pour continuer , tu poses :

$f(x)=x(1−x)1+xf(x)=\frac{x(1-x)}{1+x}$

Tu calcules f'(x) , son signe ; tu en déduis les variations de f et la valeur maximale.

$−2x(x+1)−(x−x2)(x+1)2\frac{-2x(x+1)-(x-x^2)}{(x+1)^2}$
C EST BON?

Non pour le numérateur

U(x)=x(1-x)=x-x²
U'(x)=1-2x
V(x)=1+x
V'(x)=1

Tu utilises la dérivée d'un quotient

Après calculs , tu dois trouver :

$f′(x)=−x2−2x+1(x+1)2f'(x)=\frac{-x^2-2x+1}{(x+1)^2}$

COMMENT JE FAIS POUR LA 2°

Même principe pour la 2)

Tu exprimes l'aire AEI en fonction de x : aire (AEI)=g(x)

Tu étudies les variations de g

montre moi un exemple je vois pas comment faire please

Un exemple , pas possible ...

AEI est un triangle rectangle

$\text{aire(aei)=\frac{ai\times ae}{2}$

Tu remplaces AI et AE par leurs expressions en fonction de x