Exercice sur les intégrations.

Bonjour, j'aurais besoin d'aide pour cet exercice sur les intégrations.

Voilà l'énoncé :

Nous avons deux courbes Cf et Cg

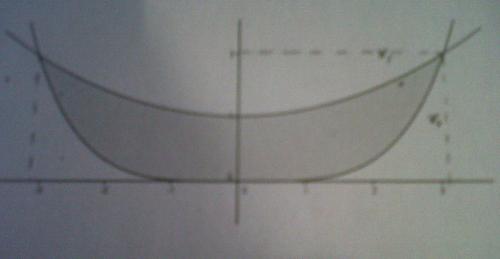
Ceci est le graphique joint a l'énoncé

Alors, il faut calculer l'aire du domaine grisé (en cm²)

Pour données, nous avons : f(x)=x²/10 et g(x)=x^4/50

Je sais comment faire, enfin je pense, mais j'ai un problème pour trouver "l'intervalle" de l'intégration, sur le dessin, on observe qu'elle ne part pas de -3 a 3 précisement, alors je sais pas comment faire, faut-il calculer f(x)-g(x).
D'autre part, je sais que ces deux fonctions sont paires, donc si l'intégrale était de -3 a 3, on aurait coupé en deux, ça aurait fait 2intégrale de 0 a 3 f(x)dx et pareil pour g(x) on les aurait calculé comme ça puis soustraites. Mais vu qu'elles ne sont pas définies sur -3/3 je ne sais pas comment faire.

Si vous pouviez m'aider... Merci

Bonjour Katherina.

À mon avis l'intervalle sur lequel tu intègres est délimité par les abscisses des points d'intersection des deux courbes, autrement dit les solutions de $x210=x450\dfrac{x^2}{10} = \dfrac{x^4}{50}$ .

Bonjour

au détail près que la fonction "du haut" est plutôt x²/10 + 1 (si je lis bien l'abscisse).

dans le corps de ce que dit Katherina, il y a aussi l'erreur de vouloir soustraire les deux aires dans le cas "pair" : il faut les ajouter au contraire.

bonne continuation.

Bonjour,

Je pense comme toi Zauctore , et les bornes d'intégration doivent être $−10-\sqrt{10}$ et $10\sqrt{10}$

Bonjour, je n'avais pas vu vos réponses, déjà merci d'avoir répondu, alors la fonction du haut c'est bien f(x), donc pour trouver les bornes, il faut que je calcule f(x)=g(x) ?

Bonjour ,

Oui , il faut bien résoudre l'équation f(x)=g(x) avec , comme l'a indiqué Zauctore

$x210+1=x450\frac{x^2}{10}+1=\frac{x^4}{50}$

D'accord je le fais toute suite, merci.

Je trouve un résultat qui n'a aucun sens. Je me suis trompée quelque part

Donne nous peut-être tes calculs.

Alors,

x²/10+1-x^4/50=0
5x²+50-x^4/50=0
x²(5-x²)+50/50=0

Après, je dois résoudre x²=0 ou (5-x²)=0 ?

Ou alors je fais pas du tout ça, et je résous -x^4+5x²+50 comme si c'était un trinome de second degrès en posant X=x² ?

Non pour ta conclusion.

$5x2+50−x450=0⟷5x2+50−x4=0\frac{5x^2+50-x^4}{50}=0 \longleftrightarrow 5x^2+50-x^4=0$

Tu ordonnes pour que ça soit plus clair

$x^4+5x^2+50=0$ (équation bicarrée )

Changement d'inconnue : $x^2=x$

Equation auxiliaire :

$x^2+5x+50=0$

Tu résous et tu trouveras deux solutionx $X_1$ et $X_2$

Ensuite , tu retournes à x en résolvant :

$x^2=x_1$ et $x^2=x_2$

Bons calculs.

Oui c'est ça que je demandais dans la dernière phrase en fait. Mais merci

Alors pour X1 je trouve -10 et X2 =5

après je fais la racine des deux c'est ça ? Ca ne devrait pas etre des solutions opposées, étant donné que les deux fonctions sont paires ?

Il y a des erreurs de signe pour X1 et X2 : revois.

Pour delta j'ai trouvé 225... Donc...

donc ?

$x1=−5−2252(−1)=.......?x_1=\frac{-5-\sqrt{225}}{2(-1)}=.......?$

$x2=−5+2252(−1)=.......?x_2=\frac{-5+\sqrt{225}}{2(-1)}=.......?$

J'espère que tu as compris tes erreurs de signe et que tu as trouvé $x_1=10$ et $x_2=-5$

Il te reste à résoudre :

$x^2=10$ et $x^2=-5$

Oui j'ai compris mon erreur, j'ai mis a positif et non negatif en fait desolée...

J'ai que besoin du x1, qui est -racine de 10 et racine de 10, parce que l'autre est negatif

Ah non c'est bon, question stupide..
Par contre, apres est ce que j'ai le droit de passer a integrale de -racine de 10 a racine de 10 de f(x)-g(x) ?

oui , mais pour simplifier le travail de calcul aux bornes , vu que le graphique est symétrique par rapport à l'axe des ordonnées , l'aire vaut :

$a=2\times \bigint_0^{\sqrt{10}} f(x)-g(x) \ dx$

En faisant je trouve 4,8 est ce que ca pourrait etre bon ?

4.8 ne peut-être qu'une valeur approchée ...il faut la valeur exacte.

Donne tes calculs si tu souhaites que l'on regarde.

( *ce serait plutôt une valeur proche de 5.9 *)

Oh excusez, moi autant pour moi, je me suis trompée dans une ligne, en corrigeant j'ai bien exactement 5.9

Merci beaucoup pour votre aide.

Attention.

5.9 n'est que la valeur approchée .

Après simplification , la valeur exacte doit être $281015\frac{28\sqrt{10}}{15}$

C'est une simplification en fait, d'accord
Merci

Donne la valeur exacte , avant la valeur approchée.

oui c'est ce que j'ai fais merci de votre aide.