Coordonnéees (centre du cercle circonscrit, orthocentre, ...)

Bonsoir à tous,

On considère un repère orthonormé (O; $i⃗\vec{i}$ , $j⃗\vec{j}$ ). Soient A(1; 1), B( $32\frac{3}{2}$ ; -2) et C(7; 2).

Faire une figure que l'on complètera tout au long de l'exercice.

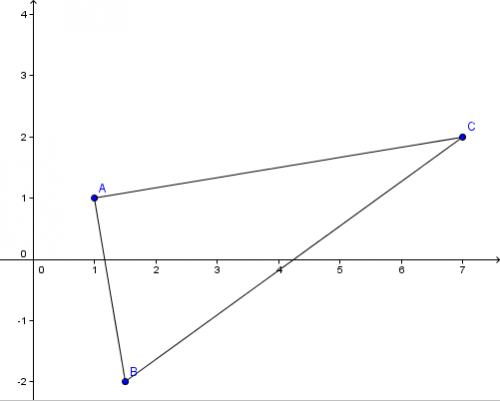
$fichier math$
2. Déterminer la nature du triangle ABC.
AB= $(xB−xA)2+(yB−yA)2\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
AB= $(32−1)2+(−2−1)2\sqrt{(\frac{3}{2}-1)^2+(-2-1)^2}$
AB= $372\frac{\sqrt{37} }{2}$

AC= $(xC−xA)2+(yC−yA)2\sqrt{(x_C-x_A)^2+(y_C-y_A)^2}$
AC= $(7−1)2+(2−1)2\sqrt{(7- 1)^2+(2-1)^2}$
AC= $37\sqrt{37}$

BC= $(xC−xB)2+(yC−yB)2\sqrt{(x_C-x_B)^2+(y_C-y_B)^2}$
BC= $(7−32)2+(2+2)2\sqrt{(7- \frac{3}{2})^2+(2+2)^2}$
BC= $1852\frac{\sqrt{185} }{2}$

Donc AB²+AC²= $374+37=1854\frac{37}{4}+37=\frac{185}{4}$
Et BC²= $1854\frac{185}{4}$
On constate que AB²+AC²=BC²
Donc d'après la réciproque du théorème de Pythagore ABC est rectangle en A.
On en déduit que la nature du triangle ABC est un triangle rectangle en A.

Déterminer les coordonnées de K centre du cercle circonscrit au triangle ABC.

Je ne comprends pas, merci de m'expliquer.

Déterminer les coordonnées de H orthocentre du triangle ABC.

Pareil pour celle-ci.

Merci à vous

Bonsoir,

Si ABC est un triangle rectangle en A où est situé le centre du cercle circoncrit au triangle ABC ?

Bonjour,

Le centre du cercle circonscrit se situe au milieu de BC

Tiens, les anciens exos de 3e !

D'après ce que tu as écrit, il te suffit de calculer els coordonnées du milieu de l'hypoténuse : ce sont les moyennes des abscisses d'une part, et des ordonnées d'autre part.

Pour la dernière question, où se situe l'orthocentre d'un triangle rectangle ?

Oui mais la géométrie :razz:

Donc avec x=xB+xC/2 et y=yB+yC/2 ?

Et pour l'orthocentre, il faut tracer la hauteur jusqu'au point A en ayant un angle droit.

$xk=32+72x_k=\frac{\frac{3}{2}+7}{2}$
$=174=\frac{17}{4}$

$yk=−2+22y_k=\frac{-2+2}{2}$
$= 0$

Donc les coordonnées de K sont $(174;0)(\frac{17}{4};0)$

Je ne trouve pas pour la question 4., 2 heures que j'essaye de chercher mais toujours rien. Merci de m'expliquer

Alors alors ah l'orthocentre est le point de rencontre des trois hauteurs... autrement dit, dès que tu connais deux hauteurs, tu sais où est l'orthocentre : à leur point d'intersection (puisque la 3e hauteur y passera aussi).

Donc je te pose ces deux simples questions pour que tu le trouves :

quelle est la hauteur relative au sommet C ?
quelle est la hauteur relative au sommet C ?
N'oublie pas que le triangle ABC est rectangle en A...

La hauteur relative au sommet C est le point A
La deuxième question c'est la même non

Citation
La hauteur relative au sommet C est le point A
une hauteur n'est pas un sommet, c'est une droite attention ! donc c'est (AC).
Citation
La deuxième question c'est la même non ?
oui, tout à fait mea culpa : - quelle est la hauteur relative au sommet
B?

Ok merci donc la hauteur relative au sommet B est la droite (BA)

Mais je ne vois toujours pas comment on fait pour l'orthocentre :frowning2:

Rho loulou, tu ne sais pas très bien lire, semble t-il ! Bon je répète :

L'orthocentre est au concours des trois hauteurs, donc de deux seulement, n'est-ce pas ? Or tu connais une hauteur (AC) et tu connais une 2e hauteur (AB)... Tu ne vois vraiment pas de point commun à ces deux droites ?

(AC) et (AB) ont un angle droit en A.

Pour la figure :

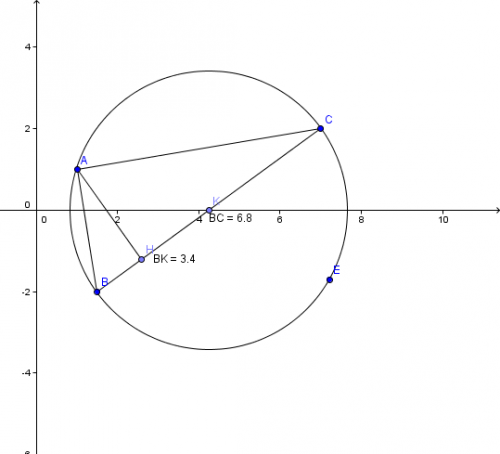
$fichier math$

l'arrondi que tu as fait afficher à geogebra est peu pertinent pour le milieu de [BC] en tout cas.

pour l'histoire des hauteurs, puisqu'on dirait que tu n'y entraves pas grand'chose : les hauteurs AB et AC se coupent en A ; l'orthocentre est donc A. la 3e hauteur est bien AH que tu as fait tracer au logiciel.

à retenir : dans un triangle rectangle, l'orthocentre est confondu avec le sommet de l'angle droit.

Je pense avoir compris, fin j'espère.

Comme l'orthocentre est au concours des trois hauteurs, donc on en déduit que le point H a pour coordonnées H(1;1).

Je sais pas si j'ai vraiment bien expliquer.