pyramide à base carrée

Bonjour,

Exercice :
SABCD est une pyramide régulière de sommet S, dont la base ABCD est un carré de côté a de centre O , et dont les quatre autres faces sont des triangles équilatéraux.

Quelle est la nature du triangle ASC ?
Donner les mesures de chacun de ses côtés en fonction de a.
Quelle est la nature du triangle ASO ?
Calculer la longueur du segment [SO], hauteur de la pyramide, en fonction de a.
Quelle est la mesure de l'angle ASO ? de l'angle ASC ?
Déduire de la question 2) le volume de la pyramide SABCD en fonction de a.
Faire un patron et une représentation en perspective cavalière de cette pyramide en prenant
a = 4 cm.

Voici mes réponses :

Le triangle ASC est un triangle isocèle.
AS = a
SC = a
AC = aV2 ???? (je suis pas sur, j'ai dit ça comme ça)

La pyramide est régulière, donc [SO] est la hauteur de cette pyramide et le triangle ASO est rectangle en O. La longueur d'une diagonale d'un carré de côté a est a√2.

OA = (a2)/2
SA² = OA² + OS²
OS² = SA² - OA² = a² - (2a²)/4 = (4a²)/4 - (2a²)/4 = (2a²)/4

OS = ((2a²)/4) = (a2)/2

Sin S = opposé / hypothénuse = ( aV2 / 2 )/ a
Sin S = V2/2
SO = AO = V2/2
dans un triangle rectangle isocèle les angles à la base sont égaux et mesurent 45°
Donc le triangle ASO est rectangle et isocèle.
le triangle AOS,est rectangle et isocèle en O et le triangle SOC est lui aussi rectangle et isocèle en O donc l'angle OSC mesure 45°
Donc :
ASC = ASO + OSC = 45 + 45 = 90°

V = (B x h )/3
V = (a² x (aV2)/2 ) /3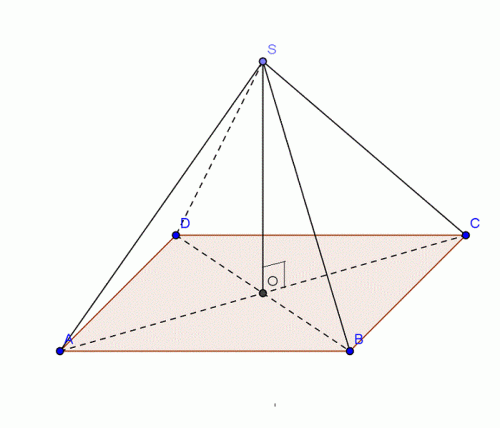

$fichier math$

Pouvez vous m'aider car je ne sais pas trop comment expliquer mes calculs, quels phrases il faut mettre et comment présenter mes calculs et il y a plusieurs calculs que je ne suis pas du tout sur et pouvez vous me dire si mes réponses sont bonnes s'il vous plait. Merci.

Bonjour,

On pourrait croire ( ou on croit ) que tu as recopié des calculs que tu n'as pas fait toi-même...!

La source :

[http://www.ilemaths.net/forum-sujet-413930.html]](http://www.ilemaths.net/forum-sujet-413930.html "http://www.ilemaths.net/forum-sujet-413930.html]")

AC=a√2 : diagonale du carré ABCD de côté a

Citation
OA = (a2)/2mal recopié : $OA=a22OA=\frac{a \sqrt 2}{2}$

Citation
OS = ((2a²)/4) = (a2)/2bizarre...

$OS2=2a24OS^2=\frac{2a^2}{4}$

$OS=a22OS=\frac{a\sqrt 2}{2}$

Pour la 4) , tu peux terminer le calcul :

$V=a326V=\frac{a^3 \sqrt 2}{6}$

Pour la 5) , il manque le patron de la pyramide.

Regarde le principe ici :

http://therese.eveilleau.pagesperso-orange.fr/pages/truc_mat/textes/pyramide.htm

Merci pour vos corrections, donc voici les réponses :

Le triangle ASC est un triangle isocèle.
AS = a car les quatre autres faces sont des triangles équilatéraux.
SC = a car les quatre autres faces sont des triangles équilatéraux.
AC² = a²+a²
AC = V(a²+a²)
AC = V(2a²)
AC = aV2 : diagonale du carré ABCD de côté a
La pyramide est régulière, donc [SO] est la hauteur de cette pyramide et le triangle ASO est rectangle en O et est isocèle.
Par Pythagore on a :
SA² = AO²+SO² <=> SO² = SA² - AO² = a² - (aV2/2)² = a² - 2a²/4 = a²/2
Donc SO = V(a²/2) = a/V2 = aV2 /2 = AO
OS = OA = aV2/2 = a / V2
Donc le triangle ASO est un triangle rectangle et isocèle en O.
Or, dans un triangle rectangle isocèle les angles à la base sont égaux et mesurent 45°
donc angle ASO (chapeau dessus) = 45°

le triangle SOC est lui aussi rectangle et isocèle en O donc l'angle OSC mesure 45°
Donc :
angle ASC = angle ASO + angle OSC = 45 + 45 = 90°
Donc le triangle ASC est isocèle en S.

V = (B x h )/3
V = (a² x (aV2)/2 ) /3
V = (a³V2)/6

Pouvez vous m'aider et me dire si les réponses sont bonnes s'il vous plait. Merci.

Cela me semble correct.

Mais pour le patron de la question 5) le mien n'était pas bon ? Je ne sais pas comment le faire.

Je ne vois pas ton patron.

Je vois une représentation en perspective cavalière.

Pour faire un patron , regarde le lien que je t'ai donné.

Le patron est le dessin à plat des faces du solide.

D'accord. Donc est ce que ce patron est bon : (le 2 ème dans l'image)

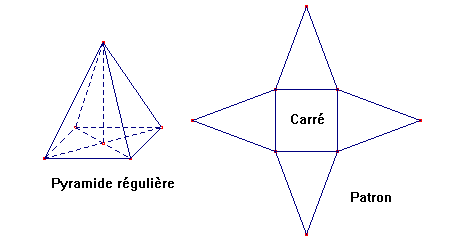
$fichier math$

Presque.

Les quatre triangles doivent être équilatéraux.

D'accord. Donc voici mon patron (fait à la main) :

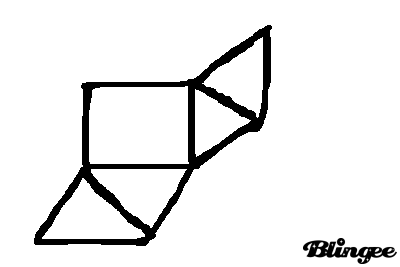
$fichier math$

Pouvez vous me dire si le patron est bon. Merci.

Si le quadrilatère est bien carré et les triangles bien équilatéraux , ça peut aller , mais le principe de patron de ton schéma précédent est plus esthétique.