Probabilités (DM)
-
Ppinceaug dernière édition par
Bonjour.
J'ai cet exercice a faire. Et je n'y arrive pas. Je vous joins l'énoncé."Une roue de loterie se compose de secteurs identiques : 3 de ces secteurs sont rouges, 4 sont blancs et n sont verts (avec n > ou égal à 1). Un joueur fait tourner la roue devant un repère fixe. Chaque secteur a la même probabilité de s'arrêter devant ce repère. Si le secteur repéré est rouge, le joueur gagne 16€. Blanc: il perd 12 €. Vert: Rejoue et si le secteur repéré est rouge il gagne 8€ ; Blanc: il perd 2 € ; s'il est vert: ne gagne rien et ne perd rien.
Soit Xn la variable aléatoire qui, à chaque partie, associe le gain algébrique du joueur.- Donner la loi de probabilité de Xn.
=> J'ai réalisé un arbre comme ci-contre:
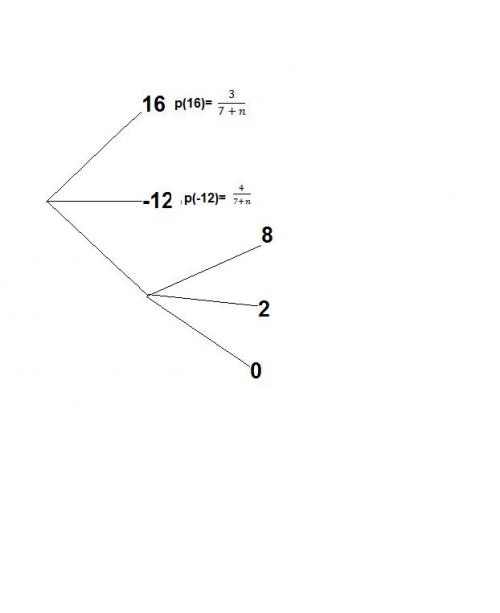
Mais comment trouver la probabilité des autres issues ? Je sais seulement qu'il faudra multiplier leur pobabilité avec celle de V soit 2/7+n.
Merci beaucoup pour votre aide.
- Donner la loi de probabilité de Xn.
-
mtschoon dernière édition par

Bonjour,
Piste pour démarrer ,
Il y a (7+n) secteurs dont n sont verts
La probabilité pour que la roue s'arrête sur le Vert est donc n7+n\frac{n}{7+n}7+nn
Ensuite ,
Sachant que la roue s'arrête sur le Vert , en rejouant , la probabilité de gagner 8 ( c'est à dire de s'arrêter sur le Rouge ) est 3n+7\frac{3}{n+7}n+73
Sachant que la roue s'arrête sur le Vert , en rejouant , la probabilité de perdre 2 ( c'est à dire de s'arrêter sur le Blanc ) est 4n+7\frac{4}{n+7}n+74
Sachant que la roue s'arrête sur le vert , en rejouant , la probabilité de ne rien gagner ni perdre ( c'est à dire de s'arrêter sur le Vert ) est nn+7\frac{n}{n+7}n+7n
Tu peux ainsi compléter ton arbre .
-
Ppinceaug dernière édition par
Merci beaucoup !
J'ai compris ! Du coup dans mon tableau de probabilités j'ai mit les deux premières que j'avais trouvé puis les votres multipliées par
\frac{n}{7+n}.
C'était ça qui me bloquait pour la suite de la question et le reste de l'exercice. A la fin j'arrive a des choses cohérentes donc cela me parrait correct.Encore merci !!!
-
Ppinceaug dernière édition par
(Escusez-moi, je n'arrive pas à faire les fractions mais c'est n/7+n)
-
mtschoon dernière édition par

C'était avec plaisir.
Une remarque pour le latex au sujet de \frac{n}{7+n} :
Tu sélectionnes \frac{n}{7+n} à la souris et tu cliques sur Latex ( en dessous du cadre texte ) ; les balises se mettent automatiquement et tu obtiens
n7+n\frac{n}{7+n}7+nn
-
Ppinceaug dernière édition par
Ah, merci ! Je me demandais à quoi pouvait bien servir ce "LaTex"...
Bonne soirée et merci pour votre aide.