Montrer que des droites sont concourantes / parallèles

Bonjour,

voici l'exercice que j'ai à faire durant ces vacances. Voici l'énoncé et ce que j'ai trouvé, pourriez vous, svp, valider mes réponses et m'amener sur le bon chemin pour les question encore incomplètes. Merci.

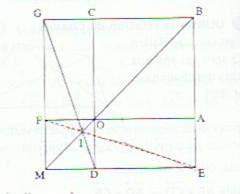
$fichier math$

OABC est un carré de côté 4 cm
M est le point défini par vec{OB} = -2 vec {OM}
(DE) et (FG) sont les parallèles passant par M aux côtés (OA) et (OC) du carré
On se propose de démontrer que les droites (OB), (GD), (FE) sont concourantes.

1- Choix d'un repère
a) Dire pourquoi ( O;1/4vec{OA};1/4vec{OC}) est un repère orthonormal.
b) Quelles sont, dans ce repère, les coordonnées des points B, G, F, D, E et les coordonnées des vecteurs et vec {OB} et {GD}

2- Détermination du point d'intersection I des droites (OB) et (GD)
a) Pourquoi les vecteurs {OI} et {OB} sont-ils colinéaires ?
b) On note (x;y) les coordonnées de I dans la question 1
Démontrer que y = x
c) en déduire, en fonction de x, les coordonnées de vec{ID}
d) Pourquoi les vecteurs {ID} et {GD} sont-ils colinéaires ?

En utilisant ce résultat, montrer que x = -1/2
e) donner les coordonnées du point I

3- La droite (FE) passe par I
En utilisant les méthodes précédentes, démontrer queles points F, I, E sont alignés.

Voici ce que j'ai trouvé :

1.a. on sait que OC = OA comme OABC est un carré. Donc 1/4 OC = 1/4 OA = 1 cm. Donc la valeur en abscisse est la meme que celle en ordonnée donc on a bien un repère orthonormal.

1.b. B est sur le meme axe parallèle à l'abscisse que C
B est sur le meme axe parallèle à l'ordonnée que A
Cela est logique puisque B est un point du carré. Comme OA = 4 et OC = 4 => B(4;4)

Coordonnées G
vec OB(4-0) OB = (4)
(4-0) (4)

Posons M(x;y) vec OM(x-0) -2 vec OM(-2x)
(y-0) (-2y)

-2x = 4 x = -2
-2y = 4 y = -2 M(-2;-2)

M est sur le meme axe parallèle à l'ordonnée que G
C est sur le meme axe parallèle à l'abscisse que G
Donc G(-2;4)

Coordonnées F
F meme axe que M
F meme axe que O
F (-2;0)

Coordonnées D
D meme axe que O
D meme axe que M
D (0;-2)

Coordonnées E
E meme axe que A
E meme axe que M
E (4;-2)

Coordonnées vec GD
(0+2) (2)
(-2 -4) (-6)

2.a. comme les points BOI sont alignés alors on peut en deduire que les vecteurs OI ET OB sont colinéaires.
Pour la démonstration je ne sais comment faire !

2.b. comme les vecteurs OI ET OB sont colinéaires et sachant que O(0;0) étant l'origine, alors les points déterminant les coordonnées sont I et B. Comme B(4;4) on voit que xB = yB alors on aura aussi xI = yI

2.c. vec ID(0 -x) (-x)
(-2 -y) (-2 -y)

2.d. comme les points G I ET D sont alignés alors on peut en déduire que les vec GD et ID sont colinéaires
pour la démonstration je ne sais toujours pas faire !

Cela est-il juste svp ?

Je bloque par la suite mais je me demande si ce ne sont pas mes resultats qui sont erronés....

Merci pour votre aide

Alors , on commence par le début , ta démonstration laisse à désirer :

( O ; 1/4vec{OA} ; 1/4vec{OC} ) est un repère orthonormé si et seulement si

les droites (OA) et (OC) sont perpendiculaires
et que
$14OA=14OA\frac{1}{4} OA = \frac{1}{4} OA$

B(4;4) c'est bien

Et pour la suite, il y a un souci : Coordonnées G : il faut nous donner 2 valeurs (coordonnée de G et ordonnée de G) tu tu donnes 4 comme réponse, c'est l'abscisse ou l'ordonnée ?

Pour la suite, j'attends tes réponses à celles)ci

oui effectivement, c'est un problème d'alignement, je voulais faire comme les coordonnées d'un vecteur (les uns sous les autres) mais cela ne fonctionne pas et je conçois que les réponses vous paraissent étranges !!

coordonnées G :
le vecteur OB (4;4)
-2 vecteur OM (-2x, -2y)
M (-2;-2)

donc G étant sur le meme axe parallèle à l'ordonnée que M alors : xM = xG = -2

G étant sur le meme axe parallèle à l'abscisse que C alors : yC = yG = 4

On a donc G (-2;4)

A demain