Déterminer la loi de probabilité d'une variable aléatoire

Voilà j'ai un DM de maths mais je bloque sur un exercice ...

L'énoncé est le suivant:
"n est un entier supérieur ou égal à 4. Dans une urne, on place n jetons : un rouge et tous les autres blancs.
On tire successivement, au hasard et avec remise, deux jetons de l'urne. On gagne 16 points si on tire deux fois le jeton rouge, 1 point si on tire deux fois un jeton blanc et on perd 5 points dans les autres cas.
X est la variable aléatoire égale au gain algébrique du joueur : X prend 16; 1 et -5"

a) Représenter cette expérience aléatoire à l'aide d'un arbre pondéré.
J'ai réussi facilement.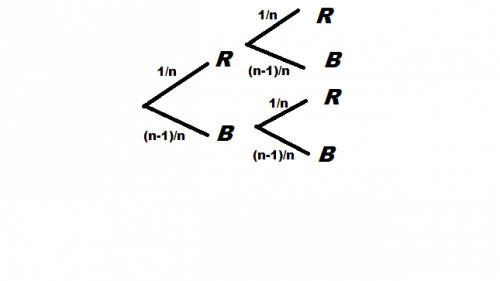

$fichier math$

b) Déterminer la loi de probabilité de la variable aléatoire X.
Ici j'ai trouvé pour

16 on a $(1n)2{(\frac{1}{n})}^{2}$
1 on a $(n−1n)2{(\frac{n-1}{n})}^{2}$
-5 on a $(1n×n−1n)2{(\frac{1}{n}}\times \frac{n-1}{n})^{2}$ je ne suis pas sur de cette dernière valeur.

c) Exprimer en fonction de n l’espérance de X.

d) Existe-t-il des valeur de n pour lesquelles le jeu est équitable ?

e) Quelles sont les valeurs de n pour lesquelles le jeu est favorable au joueur, c'est-à-dire telles que E(X)>0 ?

Je bloque pour les questions c) ; d) et e). Merci d'avance de votre aide.

Bonjour,

En effet pour la -5 il serait préférable de faire

$(1n×n−1n),+,(1n,×,n−1n){(\frac{1}{n}}\times \frac{n-1}{n}) ,+ ,(\frac{1}{n} , \times, \frac{n-1}{n})$

que le carrré