Calculs de produits scalaires dans un cube
-
NNa0h dernière édition par Hind
Bonjour!
Désolée de vous déranger par ce "beau" weekend prolongé...
J'ai un problème avec les produits scalaires...
Voici un cube qui va me servir à vous expliquer mon problème :
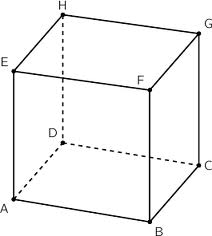
Je dois calculer le produit scalaire fa⃗.fc⃗\vec{fa} . \vec{fc}fa.fc
Je fais :
[tex]\vec{AG} . \vec{BH} = (\vec{AB} +\vec{BF}+\vec{FG}).(\vec{BF} +\vec{FG} +\vec{GH}) = \vec{AB}.\vec{BF}+\vec{AB}.\vec{FG}+\vec{AB}.\vec{GH}+\vec{BF}.\vec{BF}+\vec{BF}.\vec{FG}+\vec{BF}.\vec{GH}+\vec{FG}.\vec{BF}+\vec{FG}.\vec{FG}+\vec{FG}.\vec{GH} = 0+0+aa(-1)+aa1+0+0+0+aa1+0 = -a^2+a^2+a^2 = a^2
Mais la véritable réponse du corrigé est 3a^2 donc je ne comprend pas...
Merci d'avance!!! Bonne journée
Cordialement.
-
NNa0h dernière édition par
ag⃗.bh⃗,=,(ab⃗+bf⃗+fg⃗).(bf⃗+fg⃗+gh⃗),=,\vec{ag} . \vec{bh},=,(\vec{ab} +\vec{bf}+\vec{fg}).(\vec{bf} +\vec{fg} +\vec{gh}) ,=,ag.bh,=,(ab+bf+fg).(bf+fg+gh),=,
ag⃗.bh⃗,=,ab⃗.bf⃗+ab⃗.fg⃗+ab⃗.gh⃗+bf⃗.bf⃗+bf⃗.fg⃗+bf⃗.gh⃗+fg⃗.bf⃗+fg⃗.fg⃗+fg⃗.gh⃗\vec{ag} . \vec{bh}, =,\vec{ab}.\vec{bf}+\vec{ab}.\vec{fg}+\vec{ab}.\vec{gh}+\vec{bf}.\vec{bf}+\vec{bf}.\vec{fg}+\vec{bf}.\vec{gh}+\vec{fg}.\vec{bf}+\vec{fg}.\vec{fg}+\vec{fg}.\vec{gh}ag.bh,=,ab.bf+ab.fg+ab.gh+bf.bf+bf.fg+bf.gh+fg.bf+fg.fg+fg.gh
ag⃗.bh⃗,=,0+0+a<em>a</em>(−1)+a<em>a</em>1+0+0+0+a<em>a</em>1+0=−a2+a2+a2=a2\vec{ag} . \vec{bh}, =, 0+0+a<em>a</em>(-1)+a<em>a</em>1+0+0+0+a<em>a</em>1+0 = -a^2+a^2+a^2 = a^2ag.bh,=,0+0+a<em>a</em>(−1)+a<em>a</em>1+0+0+0+a<em>a</em>1+0=−a2+a2+a2=a2
*Modif de Zorro : quelques espaces pour que cela rentre dans une fenêtre *
-
NNa0h dernière édition par
Désolée pour les calculs qui sont mal sortis, je les ai réécrits ci-dessus.
Merci!
-
Zorro dernière édition par

bonjour,
J'ai envie de répondre comme toi !
Mais je vais faire les calculs sur un papier sans les tiens et je reviens !
-
Zorro dernière édition par

Je ne mets pas les flèches FA sera écrit à la place de fa⃗\vec {fa}fa
J'ai fait plus simple que toi
FA.FC = (FB+BA) . (FB+BC)
FA.FC = FB² + FB.BC + BA.FB + BA.BC
FA.FC = a² + 0 + 0 + 0 = a²
Quelle est l'origine de la réponse 3a² ?
-
Zorro dernière édition par

Si la question est : calculer FA.FC pourquoi tu calcules AG.BH ?
Tu donnes le bon énoncé !
-
NNa0h dernière édition par
Zorro
Si la question est : calculer FA.FC pourquoi tu calcules AG.BH ?Tu donnes le bon énoncé !
Mince! Je suis désolée c'est une erreur, je voulais écrire AG.BH bien sur!
J'avais pas mal de calculs sur ma feuille, j'ai dû m'enmêler ls pinceaux...C'est bien AG.BH que je cherche à calculer.
-
NNa0h dernière édition par
Zorro
Je ne mets pas les flèches FA sera écrit à la place de fa⃗\vec {fa}faJ'ai fait plus simple que toi
FA.FC = (FB+BA) . (FB+BC)
FA.FC = FB² + FB.BC + BA.FB + BA.BC
FA.FC = a² + 0 + 0 + 0 = a²
Quelle est l'origine de la réponse 3a² ?
La réponse 3a² est celle de mon prof de maths...
Il raisonne comme ça :
ag⃗.bh⃗=(af⃗+fg⃗).(bf⃗+fh⃗)\vec{ag} . \vec{bh} = (\vec{af} +\vec{fg} ).(\vec{bf} +\vec{fh} )ag.bh=(af+fg).(bf+fh)
=af⃗.bf⃗+af⃗.fh⃗+fg⃗.bf⃗+fg⃗.fh⃗= \vec{af} .\vec{bf} + \vec{af} .\vec{fh} +\vec{fg} .\vec{bf} +\vec{fg} .\vec{fh}=af.bf+af.fh+fg.bf+fg.fh
=fa⃗.fb⃗+a2+0+fg⃗.fg⃗=a2+a2+0+a2=3a2= \vec{fa} .\vec{fb} + a^2 + 0 + \vec{fg} .\vec{fg} = a^2 + a^2 +0+ a^2 = 3a^2=fa.fb+a2+0+fg.fg=a2+a2+0+a2=3a2Mais il y a plusieurs étapes que je ne comprend pas...
Comme quand il passe de FG.FH à FG.FG ou quand il écrit que FA.FB = a²Peut-être qu'il s'est trompé dans la correction, mais ça m'étonnerait...