Cône et cylindre
-
Sserenade dernière édition par
bonjour
j'ai besoin d'explications pour mon DM s'il vous plaît.
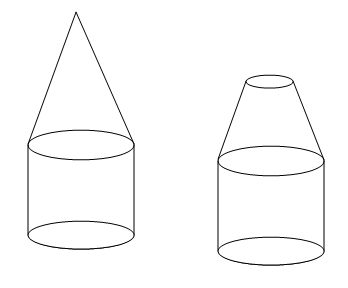
Merci de votre aideUn réservoir est constitué d'un cylindre de rayon de base r et de hauteur h et d'un cône de révolution de même rayon de base et de hauteur h' = 3h / 2.(Voir figure).
- Montrer que le volume de ce cylindre est le double de celui du cône.
- a) Calcule la hauteur h' du cône pour que le volume du réservoir soit 528 cm³.
b) Pour créer une ouverture du réservoir on coupe le cône à mi-hauteur parallélement au plan à sa base. On obtient un réservoir ayant la forme indiquée par la figure ci-dessous: Calculer le voume restant du réservoir.
On donne Pi = 22/7.
J'ai fait la question 1 j'ai trouvé:
πr² x h = 2πr² x h'Mais je coince à la question 2a) Comment calculer h'????
-
mtschoon dernière édition par

Bonjour,
Le volume du cylindre est $\text{V=\pi \times r^2\times h$
Le volume du cône est : $\text{V'= \frac{1}{3} \times \pi r^2 \times h'= \frac{1}{2} \times \pi r^2 \times h$
Pour le 2)a) :
V+V′=528V+V'=528V+V′=528<=>π×r2×h + 12×πr2×h=528\pi \times r^2\times h\ +\ \frac{1}{2} \times \pi r^2 \times h=528π×r2×h + 21×πr2×h=528
Tu obtiens ainsi : 32πr2h=528\frac{3}{2}\pi r^2 h=52823πr2h=528
Tu sais que32h=h′\frac{3}{2}h=h'23h=h′ donc :
πr2h′=528\pi r^2 h'=528πr2h′=528
Tu termines pour obtenir h'
-
Sserenade dernière édition par
πR2h' = 528
h' = 528 / πR2
h' = 528 / (352/7)
h' = 10,5
-
Sserenade dernière édition par
est ce que mon résultat de h' est bon?
-
mtschoon dernière édition par

Oui pour h′=528πr2h'=\frac{528}{\pi r^2}h′=πr2528
Pour la réponse finale que tu donnes , tout dépend de la valeur r et...la valeur de r ...je ne la vois pas écrite...
-
Sserenade dernière édition par
Calculons la hauteur du cone réduit
sa hauteur est: 10,5 / 2 =5,25
Calculons le volume du cone initial
V = 1/3 B x h
V = 1/3 x 5² x π x 10,5
V = 87,5π cm³Est ce que j'ai bon jusque là
-
Sserenade dernière édition par
C'est une erreur de ma part on a écrit
Dans la suite on donne r = 4 cm
-
mtschoon dernière édition par

Pour r=4 , h'=10.5 est bon.
Pour le volume du cône initial , ce 5² est bizarre...car r ne vaut pas 5 ( tu as indiqué qu'il valait 4... )
-
Sserenade dernière édition par
Oui c'est bien r=4
je reprends alors
V = 1/3 x 4² x 22/7 x 10,5
V = 176 / 3 cm³k = 1/2
V' = (1/2)³ x 56π
V' = 1/8 x 176/3
V' = 22/3 cm³Volume restant du réservoir
V restant = V total - V'
V restant = 528 - (22/3)
V restant = 1562/3Voilà ce que j'ai sauf distraction de ma part
-
mtschoon dernière édition par

Pour V , ta première formule est exacte , mais je ne comprends pas ce 176 / 3comme réponse.
Idem pour V'.
-
Sserenade dernière édition par
J'ai laissé comme ça parce que je me suis dit que dans l'énoncé on ne nous a pas dit d'arrondir ou de données une valeur approchée...
Fallait-il arrondir?
-
Sserenade dernière édition par
V = 176 cm3
V' = 1/8 x 176
V' = 22 cm3Volume restant du réservoir est:
Vr = 528 - 22
Vr = 506 cm3
-
mtschoon dernière édition par

Cette fois , les résultats sont bons !
-
Sserenade dernière édition par
Merci mtschoon et bonne nuit à tous
-
mtschoon dernière édition par

Bonne nuit à toi serenade.