Pyramide et diabolo

Bonsoir alors voilà, j'ai un exercice à faire que je ne comprend pas, je sais pas si c'est à l'aide d'une formule ou quoi que ce soit, si quelqu'un peut m'aider, je vous en remercie d'avance.

Exercice:

Un parfumeur souhaite conditionner un nouveau parfum dans un flacon original d'une contenance de 200 cm3. Un verrier lui propose les deux formes suivantes: un diabolo de rayon 3 cm et une pyramide à base carrée d'arête 5 cm reposant sur un pavé droit de 1 cm de haut.

Pour limiter les frais d'emballage, le parfumeur souhaite que le flacon soit le moins haut possible, quelle forme doit-il alors choisir ?

Bonjour,

Il faudrait savoir ce qu'on appelle le solide diabolo , moi je connais les parallélépipèdes rectangles, les cubes, les cônes, les pyramides, les boules, les cylindres .. mais pas les diabolos

sinon les diabolos menthe j'aime bien

De la même forme que celui là

Bonjour Zorro et Meloou ,

J'ai récupéré une image dans un viel énoncé. J'espère qu'elle correspond...

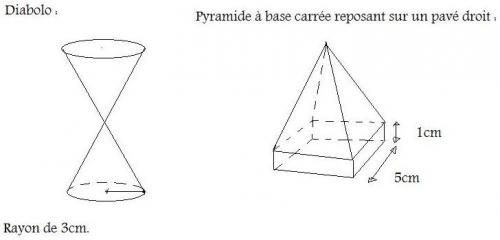
$fichier math$

Bonjour mtschoon, oui voilà c'est exactement comme sa ! Merci !

Je ne sais pas comment m'y prendre

Vu que le schéma est le bon , je te mets sur la voie.
Si Zorro passe par là , elle continuera peut-être.

Tu peux appeler h la hauteur du diabolo est h' celle de l'autre solide.
Connaissant le volume , tu peux trouver h et h' et les comparer.

Je te donne la piste pour le diabolo :

Le diabolo est composé de 2 cônes ( de hauteur h/2 chacun )
Je suppose que le parfum peut être mis dans chacun des 2 cônes.
Le volume de chaque cône est $100cm^3$

Le volume d'un cône est (1/3) x aire de la base x hauteur

L'aire de la base vaut ∏r² ( r étant le rayon )

Ici , tu obtiens donc :

$13×π32×(h2)=100\frac{1}{3} \times \pi 3^2 \times (\frac{h}{2}) = 100$

Tu résous cette équation pour trouver h

Ensuite , tu travailles sur l'autre solide.