Devoir sur produit scalaire

Bonsoir

Voici le texte du devoir. Je bute sur la question 3)
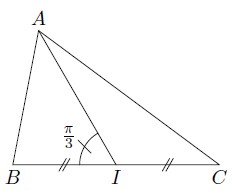
ABC est un triangle et I est le milieu de [BC].
On donne BC = 4, AI = 3 et $(ia⃗,ib⃗)=π3(\vec{ia},\vec{ib})=\frac{\pi}{3}$

Calculer :

$ab⃗.ac⃗\vec{ab}.\vec{ac}$
$ab^2 + ac^2$
$ab^2 - ac^2$
AB et AC
En utilisant la relation de Chasles, j'ai trouvé $ab⃗.ac⃗=5\vec{ab}.\vec{ac}=5$
Le théorème de la médiane permet de trouver 26 à la question 2)
Je ne sais pas faire
$ab^2=7 ;et; ac^2=19$
en utilisant le système d'équation à 2) et 3)

Merci de me donner une piste pour la question 3
Bonne soirée

Lexot2

figure d'un triangle

Bonsoir,

Je regarde le 3)
Piste,

$ab2−ac2=ab⃗2−ac⃗2=(ab⃗+ac⃗)(ab⃗−ac⃗)ab^2-ac^2=\vec{ab}^2-\vec{ac}^2=(\vec{ab}+\vec{ac})(\vec{ab}-\vec{ac})$

$ab⃗+ac⃗=2ai⃗\vec{ab}+\vec{ac}=2\vec{ai}$ ( avec la relation de Chasles )

$ab⃗−ac⃗=ab⃗+ca⃗=ca⃗+ab⃗=cb⃗\vec{ab}-\vec{ac}=\vec{ab}+\vec{ca}=\vec{ca}+\vec{ab}=\vec{cb}$

Donc : $ab2−ac2=2ai⃗.cb⃗ab^2-ac^2=2\vec{ai}.\vec{cb}$

Il te reste à calculer ce produit scalaire.

Bonsoir,

Merci pour la piste. J'avais utilisé :
$ab2−ac2=ab⃗2−ac⃗2=(ai⃗+ib⃗)2−(ai⃗+ic⃗)2ab^2-ac^2=\vec{ab}^2-\vec{ac}^2=(\vec{ai}+\vec{ib})^2-(\vec{ai}+\vec{ic})^2$
et je trouvais 0.
Pourquoi cette méthode plus lourde que la tienne n'a pas marché ?
Encore merci pour ton soutien

Bonsoir

J'ai trouvé mon erreur. L'expression donne ceci :
$(ai⃗+ib⃗)2−(ai⃗+ic⃗)2=(\vec{ai}+\vec{ib})^2-(\vec{ai}+\vec{ic})^2=$
$2ai⃗.ib⃗−2ai⃗.ic⃗=2ai⃗.cb⃗=2\vec{ai}.\vec{ib}-2\vec{ai}.\vec{ic}=2\vec{ai}.\vec{cb}=$
$\times ai\times cb \times cos(\vec{ai},\vec{cb})=$
$\times ai\times cb \times \frac{-1}{2}=-12$

Encore merci pour toute l'attention apportée à mon post
Bon week-end

lexot2

La réponse à trouver est bien -12.

Bon week-end à toi !