Etablir un arbre pondéré et calculer la probabilité de réussite

[david06]

Bonjour à tous,

Un joueur débute un jeu vidéo et effectue plusieurs parties successives. On admet que :
• la probabilité qu'il gagne la première partie est de 0,1 ;
• s 'il gagne une partie, la probabilité de gagner la suivante est égale à 0,8 ;
• s'il perd une partie, la probabilité de gagner la suivante est égale à 0,6.

On note pour tout entier naturel compris entre 1 et 3, les événements:
Gn: "le joueur gagne la n-ième partie"
(c'est-à-dire par exemple G1 est l'événement: "le joueur gagne la 1ère partie"...)

1. Établir un arbre pondéré traduisant la situation.

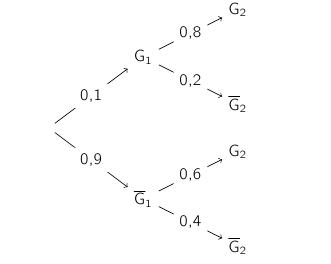
2. Calculer la probabilité que le joueur gagne la seconde partie.

P(G2)=P(G1∩G2)+P(G1Barre∩P2)=0,10,8+0,90,6=0,62
Pg2(G1barre)=P(G2∩G1 barre)/P(G2)=0,9*0,6/0,62≈0,87

La probabilité que le joueur gagne la seconde partie est d'environ 0,87.

3. Calculer la probabilité que le joueur gagne au moins une partie.

On calcule d'abord la probabilité de l'événement contraire: "le joueur gagne au moins une partie".
P(C1barre∩G2∩G3barre)=0,90,40,4=0,144
Donc la probabilité de l'événement recherché est : 1-0,144=0,856

Merci pour votre aide.

[Zorro]

Bonjour,

Ton arbre est juste.

Pour la 2 ton écriture est difficile à comprendre ....

P(G2)=P(G1∩G2)+P(G1Barre∩P2)=0,10,8+0,90,6=0,62 devrait plutôt être

P(G2)=P(G1∩G2)+P(G1Barre∩G2)=0,10,8 + 0,90,6 =0,62

Pg2(G1barre)=P(G2∩G1 barre)/P(G2)=0,9*0,6/0,62≈0,87

doit être $P_{G2}$(G1barre) = P(G2∩G1 barre)/P(G2) = 0,9*0,6/0,62 ≈0,87

On calcule d'abord la probabilité de l'événement contraire à l'évènement "le joueur gagne au moins une partie" : quel est cet évènement ? tu ne le dis pas , donc ta démonstration tombe à l'eau !

P(C1barre∩G2∩G3barre) est du domaine du délire .... C1 et G3 apparaissent ici comme des cheveux sur la soupe !

Pourrais tu te relire avant d'envoyer ?