hauteur d'un cône - fonction -

Bonjour, Merci de m'aider.
Le schèma ci dessous représente une sphère creuse de diamètre [AB] dans laquelle est inscrit un cône de sommet A, d'axe (AB) et [MH] un rayon du cercle de base.
O est le centre de la sphère et le segment [MB] est figuré car il est nécéssaire à la résolution du problème.
Il s'agit de déterminer la hauteur du cône donnant le volume maximal, on note :
-R le rayon de la sphère.
-h la hauteur [AH] du cône.
-x le rayon HM du cône.

1°
a)Démontrer que l'angle HAM est égal a l'angle HMB soit : HAM=HMB.
b)Démontrer que HB/HM=HM/HA.
c)En déduire que x²=h(2R-h).

2°Exprimer le volume V du cône en fonction de h.
3°On note f la fonction définie sur [0;2R] qui à tout h associe le volume V du cône.
a)Calculer la dérivée de f.
b)En déduire les variation de f.
c)Donner le volume maximal Vm du cône inscrit dans la sphère, en fonction de R.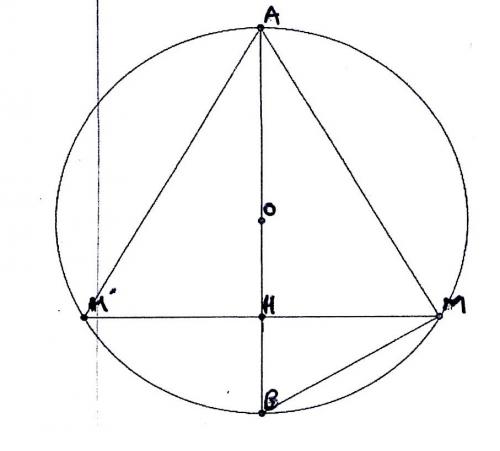

Schèma de l'exo !

Bonjour,

Piste pour démarrer,

$\text{\widehat{ham}=\widehat{bam}=\widehat{bam'} : angle inscrit qui intercepte l'arc \overset\frown{m'b}$

$\text{\widehat{hmb}=\widehat{m'mb} : angle inscrit qui intercepte l'arc \overset\frown{m'b}$

Deux angles inscrits qui intreceptent le même arc sont égaux donc :

$\text{\widehat{bam'}=\widehat{m'mb} donc ......$

Donc AHM=BAM, merci beaucoup !!
Pour la question b) comment puis-je faire ?

Idée :

Tu justifies que les triangles rectangles HMB et HAM ont deux angles respectivement égaux donc ils sont semblables , donc leurs côtés sont respectivement proportionnels

Ecris la proportionalité des côtés.

J'ai essayé de l'écriture mais sa me donne du : (1/3*h)/x=x/h est-ce ça ?

Tu dois d'abord écrire ( ou tu as peut-être écrit

$\text{\frac{hm}{ha }=\frac{hb}{hm}$

HA=h
HM=x
HB=AB-AH=2R-h

En remplaçant et en faisant les produits en croix , tu dois obtenir l'égalité demandée dans ton énoncé.

J'ai bien tout trouvé, aprés pouvez-vous m'aider pour la 2) et la 3) svp ?

Le volume d'un cône vaut (1/3).Aire de la base.Hauteur

Le volume V du cône vaut donc :

$\text{v=\frac{1}{3}\times (\pi hm^2)\times ah$

Tu remplaces HM et AH par leurs valeurs

Tu auras ainsi une fonction de variable h à étudier.

La fonction que je doit trouver est-elle (-πh²+2rh)/3 ?

Vérifie peut-être.

$v=13πx2hv=\frac{1}{3}\pi x^2 h$

Tu remplaces x² par la valeur trouvée au 1)c)

Ah merci !!

Je n'arrive vraiment pas la 2 et 3)a)b)c) j'ao besoin d'aide, surtout pour savoir si ce que j'ai fait est bon car je suis perdue

Qu'à tu fais de nouveau ?

Fais ce que je t'ai indiqué dans mon précédent message V=... et remplace x² par l'expression trouvée au 1)c)

Si tu veux que nous vérifions , donne tes calculs.

Aire base = πr²
=πx²
=π(h(2R-h))
Aire base = π(2Rh-h²)
Ainsi : Vcône = 1/3*π(2Rh-h²)*h
=(π(2Rh-h²)*h)/3=(2πRh²-πh³)/3
Est-ce sa le volume du cône ?

Oui , mais pour l'étude , ce sera plus simple en mettant ∏ en facteur :

$v=f(h)=13π(2rh2−h3)v=f(h)=\frac{1}{3}\pi(2rh^2-h^3)$

Maintenant , tu calcules f'(h) ( R est une constante )

f'(h)=π(Rh-3h²)*1/3 ?

La dérivée de h² est 2h donc ...tu recomptes.

soit : f'(h) = 1/3*π(4Rh-3h²) c'est bien sa ou pas ?

C'est ça.

Tu peux mettre h en facteur :

$f′(h)=13πh(4r−3h)f'(h)=\frac{1}{3}\pi h(4r-3h)$

Vu que h >0 , f'(h) est du signe de (4R-3h)

Quand j'utilise mes formule de cours, pour calculer f'(h) sachant que l'équation est de la forme u/v sa fait : (u'v-uv')/v² et je ne trouve plus ce résultat pourquoi ?

Pour moi je suis d'acord avec ce que vous m'indiquer comme résultat sauf le -3h ne serai t-il pas plutot un -3h² ?

As tu compris , comme je te l'ai indiqué , que j'ai mis h en facteur ?

La dérivée de u/v n'est pas utile ici !
Si tu veux l'utiliser , n'oublie pas que la dérivée d'une constante vaut 0.

Indique tes calculs si tu veux que nous les vérifions.

En faite j'ai parlé trop vite et j'ai bien trouvé le même résultat avec la dérivée de u/v parce que je n'avai pas factorisé.
Le tableau de signe de f' comment je le dresse ?

Je te l'ai déjà indiqué :

Citation
Vu que h >0 , f'(h) est du signe de (4R-3h)

Oui mais comment je calcul en quel valeur sa s'annule ?

Tu ne sais pas cela ?

Pour h compris entre 0 et 2R ( car H compris entre A et B ) :

$\leftrightarrow 3h=4r \leftrightarrow h=\frac{4r}{3}$

$\lt 0 \leftrightarrow 3h\gt 4r \leftrightarrow h\ge \frac{4r}{3}$

$\gt 0 \leftrightarrow 3h\lt 4r \leftrightarrow h \lt \frac{4r}{3}$

Ah oui merci; donc pour calculer Vmax on remplace h par 4R/3 dans la fonction f ?

oui.