Hyperbole
-
Hhanabi dernière édition par
Bonjour,
Je dois faire cet exercice: "déterminer une équation cartésienne de l'hyperbole équilatère de centre (0,0), admettant la droite (1 1 0) pour asymptote et comprenant (-5, 13). Quels en sont les sommets?"
J'ai fait le calcul mais j'arrive à des choses étranges.
J'obtiens que 25-169= a² ????
Pourriez-vous m'aider à faire cet exercice. Merci
-
mtschoon dernière édition par

Bonsoir,
Je trouve ton énoncé un peu confus...
Le point de coordonnées (-5, 13) doit être sur l'hyperbole .
Je pense que tu n'as pas pris la "bonne " hyperbole équilatère , ce qui fait que tu trouves 25-169=a²
Prends l'hyperbole d'équation y²-x²=a²
Tu obtiens ainsi 169-25=a² <=> a²=144
L'équation est y²-x²=144
Les asymptotes ont pour équation y=x et y=-x
Les "sommets" sont les points de l'hyperbole d'abscisse 0
Tu obtiens donc (0,12) et (0,-12)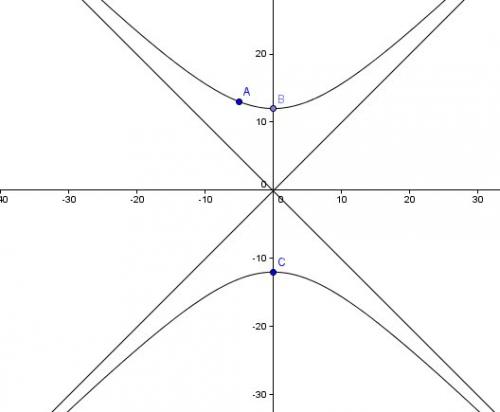
-
Hhanabi dernière édition par
D'accord merci beaucoup et pardon pour ma confusion

-
mtschoon dernière édition par

Pas de problème !
Si j'ai bien compris ce que tu voulais dire , c'est très bien.