Devoir passerelle 3ème-seconde : aire en fonction de x

Bonsoir tout le monde !
Alors j'aurais besoin d'un petit coup de main...

J'ai un devoir passerelle de mathématiques à faire, mais je bloque sur une question...
La voici :

Je me situe dans un triangle rectangle AHE, rectangle en H. Le côté HA = 6-x cm, et le côté HE = x cm.
Sachant tout ceci, il faut que je déduise l'aire de ce triangle en fonction de x, puis l'aire de la partie grisée que je noterai f(x), qui n'est autre que ce même triangle et un autre triangle qui lui est strictement identique.

Je vous montre mes calculs :
L'aire d'un triangle = ch/2.
Donc : Aire AHE = x(6-x)/2 = (6x-x²)/2 = 1/2(6x-x²) = 3x-1/2x²

Mais sur un forum, une personne cherchant de l'aide comme moi trouve elle ceci : ( x multiplié par 6-x) /2 = 6x-x /2 = 3x - x/2.

Quelqu'un pourrait m'éclairer, c'est l'embrouille totale dans ma tête...
Merci d'avance !

Bonjour,
Ton calcul pour l'aire du triangle AHE est juste, mais place des parenthèses :
3x - (1/2)x²
Pour la suite (partie grisée), il faudrait joindre une figure.

$fichier math$
mathtous
Bonjour,
Ton calcul pour l'aire du triangle AHE est juste, mais place des parenthèses :
3x - (1/2)x²
Pour la suite (partie grisée), il faudrait joindre une figure.

Bonjour,

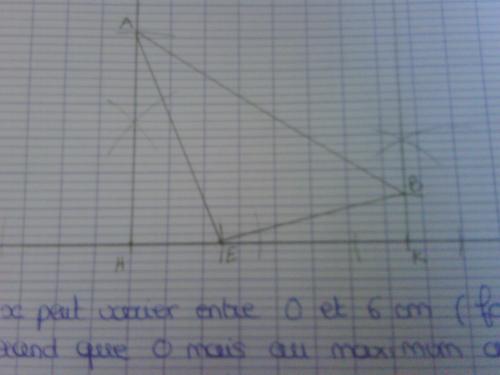
merci beaucoup ! je vais joindre à ma réponse une photo de la figure que j'ai réalisé. La partie grisée est : le triangle AHE + BEK.

Merci de votre aide !

Précise l'énoncé et ce qu'on te demande.
Apparemment, BEK est rectangle en K, BK = x, et EK = 6-x (HK = 6) ?
L'aire grisée est donc le double de celle du triangle AHE.
Alors que vaut f(x) ?
Et quelles sont les questions suivantes ?

mathtous
Précise l'énoncé et ce qu'on te demande.
Apparemment, BEK est rectangle en K, BK = x, et EK = 6-x (HK = 6) ?
L'aire grisée est donc le double de celle du triangle AHE.
Alors que vaut f(x) ?
Et quelles sont les questions suivantes ?

Merci beaucoup pour toute votre aide en fait j'ai réussi à m'en sortir ! Merci !

De rien.
A+