déterminer les dimensions d'une poutre
-
NNomatom dernière édition par
Lorsqu'on veut équarrir un tronc d'arbre de manière à donner à la poutre obtenue la plus grande résistance possible à la flexion, on se garde bien de lui donner une section carrée, mais on la rend toujours plus haute que large.
Si la base est de largeur x et la hauteur est h, on montre en mécanique que la résistance est d'autant plus grande que x²*h est grand.
Le tronc d'arbre utilisé est de diamètre 3 mètres.Déterminer x et h, en décimètres, pour que la poutre ait le maximum de résistance à la flexion.
edit : merci de donner des titres significatifs
-
mtschoon dernière édition par

Bonjour,
Pour respecter les notation usuelles ( inconnue de travail x ) , j'aurais écrit xh² au lieu de x²h pour calculer h² de façon simple en fonction de x et faire l'étude en fonction de x. Vérifie .
Tu as un schéma en coupe de ce type :
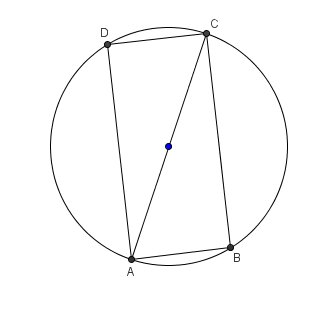
En mètres :AB=x (x > 0)
BC=h (h > 0)
AC=3Théorème de Pythagore : AB²+BC²=AC² < = > x²+h²=9 <=> h²=9-x²
Ensuite , si c'est xh² , tu peux évaluer ainsi : xh²=x(9-x²)
Tu poses f(x)=x(9-x²)
Tu étudies les variations de f pour x > 0 et tu en déduis le maximum.
si c'est x²h ( comme tu l'écris ) qu'il faut évaluer : x²h=(9-h²)h
Tu poses g(h)=h(9-h²)
Tu étudies les variations de g pour h > 0 et tu en déduis le maximum.
*Attention : dans ces calculs , les valeurs de x et h sont en en mètres . il faudra convertir tes résultats en décimètres *