étude sur une parabole

$fichier math$ Bonjour, j'ai un dm pour lundi et j'i du mal, alors voila :

a) Déterminer les signes de a et de delta. Justifier.
b) Determiner le nombre C
c) Determiner les racines de f.
Soit l'équation f(x)=m ou m est un réel. Determiner suivant les valeurs de m, le nombre de solutuions de cette équation.
Comparer si possible les images de 2√2 et √3.
On admet que f(x)=(x-a)²+ beta
Determiner les deux reels alpha et beta . Justifier.
b) En deduire que f(x)=x²-2x-8

Alors j'ai trouvé a est positif car le sommet est vers le bas, delta positif car il admet 2 solutions.
b) C=-8
Je bloque pour la question C, merci de m'aider :frowning2:
Demandez moi la courbe par email v.morgan59660@hotmail.fr s'il vous plait, je n'arrive pas a mettre l'image

edit : merci de mettre des titres significatifs

Bonjour,
Si on avait le début de l'énoncé, on pourrait peut-être t'aider.
Pour placer une image, regarde en bas , avant "envoyer", en bleu : "ajoute une image".

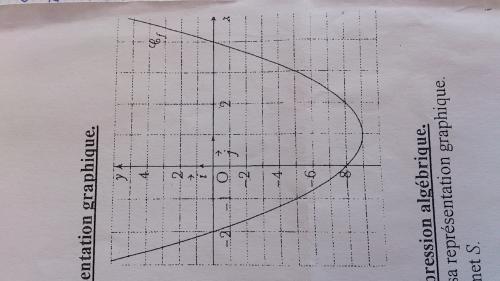
debut: representation graphique d'une fonction f definie sur R par :
f(x)=ax²+bx+c ou a, b et c sont des reels differents de 0. delta est le discriminant du trinome f

$fichier math$
C'est plus facile si on met la figure à l'endroit ...
La fonction est décroissante, puis croissante : cela fournit le signe de a.
La courbe coupe l'axe des abscisses, donc f admet 2 racines distinctes : cela donne le signe de Δ.

Merci et pour determiner la racine de f ?

"Les" racines de f ?
On les lit sur le graphique.
Mais répond d'abord à la question 1)a)

ils sont tous les deux positifs.
c=-8.
c'est pour determiner les racines de f que je ne comprends pas

La courbe a pour équation y = f(x)
Elle coupe l'axe des abscisses lorsque y = 0, ce qui correspond à l'équation f(x) = 0 donnant les racines.
Or, regarde le dessin : où la courbe coupe-t-elle l'axe des abscisses ?

en -2 et en 4, je comprends toujours pas..

f(x) est de la forme f(x) = ax² + bx + c
Pour trouver c = -8, tu as remplacé x par 0 et tu as lu sur le graphique que y vaut alors -8.
Autrement dit, tu as cherché l'intersection de la courbe avec l'axe des ordonnées.
Pour trouver les racines de f, c'est le contraire : ce sont les abscisses des points d'intersection avec l'axe des abscisses, correspondant à y = 0 (les points de l'axe des abscisses ont une ordonnée nulle).

Oulah je ne comprends pas du tout la

Soit f(x) = x² - 2x - 8.
Sa représentation graphique est une parabole.
Calcule :
a) les coordonnées du point d'intersection de cette parabole avec l'axe des ordonnées.
b) les coordonnées du point d'intersection de cette parabole avec l'axe des abscisses.

a) -8
b) -2; 4
C'est ca non ?

Presque : je demandais les coordonnées.
a) (0;-8)
b) (-2;0) et (4;0).

Pour a), tu remplaces x par 0,
Pour b) tu résous f(x) = 0 (ou y = 0 si on pose y = f(x))

Ah je pense avoir compris, merci beaucoup !!

Tu sais faire la suite ?

non pa

Citation
c) Determiner les racines de f.Ça, tu as compris ?

Citation
2) Soit l'équation f(x)=m ou m est un réel. Determiner suivant les valeurs de m, le nombre de solutions de cette équation.Utilise le graphique donné : trace la droite d'équation y = m. Regarde à quelle condition elle coupe ou pas la courbe.

Comment est une droite dont l'équation est y = m ?

Si m < -9 , pas de solution
Si m = -9 : une solution
Si m > -9 : 2 solutions distinctes.
Ça t'apporte quoi ?

Desolé mais je ne saisis toujours pas, c'est compliqué..

Pour comprendre ma réponse ci-dessus, tu dois faire l'effort de suivre les précédents conseils :
Trace la droite d'équation y = m (sur le même graphique que la parabole).
Que peut-on dire de cette droite (elle est comment ?)

Mais comment tracer la droite m ?

C'est précisément ce que je te demande.
La droite d'équation y = m est particulière : elle est parallèle à ...

a l'axe des abscisses ?

Oui, et elle se situe plus ou moins haut selon la valeur de m.
Tu vois que si elle est trop basse (m < -9) elle ne coupe pas la parabole
Si m = -9, elle lui est tangente
Et si m > -9 , elle la coupe en deux points.

Ps : désolé, j'avais écrit 8 au lieu de -9 !? (moi aussi je fatigue ...).

C'est pas grave ca !
elle coupe en deux (-2;0) (4;0)

Ça, c'est pour m = 0 : l'axe des abscisses.

Je fais un dessin avec m = -5 : la droite d'équation y = -5 est en rouge : elle coupe la parabole en deux points (peu importe leurs abscisses).

$fichier math$
J'en dessine une autre, en vert, pour m = -10 : elle ne coupe pas la parabole.

aaaaaah je comprends, mais comment sait-on la valeur e m dans ce cas la ?

Relis la question :
Citation
Determiner suivant les valeurs de m, le nombre de solutions de cette équation.On ne cherche pas une valeur de m, on cherche à dire quand il y a ou pas des solutions.
Je reprends :
Si m < -9 : la droite ne coupe pas la courbe, l'équation f(x) = m n'a donc pas de solutions.
Si m = -9, la droite est tangente à la courbe en un seul point : l'équation admet une seule solution.
Si m > -9 : la droite coupe la courbe en deux points : l'équation admet deux solutions distinctes.
Tu vois que toutes les valeurs possibles de m sont envisagées.

donc l'equation admet deux solutuions distinctes

Pas toujours : ça dépend de m.
Elle admet 2 solutions lorsque m > - 9.

On n'aura pas le temps de voir toutes les questions.
Pour la suivante, remarque que 2√2 (=√8) et √3 sont toutes deux plus grandes que 1.
Or, en regardant une fois de plus le dessin, on voit que la fonction est croissante sur l'intervalle [1;+∞[.
Qu'en résulte-t-il pour les images de 2√2 et √3 ?