valeurs absolues Raisonnement par disjonction des cas

Bonjour j'aurais besoin d'aide pour mon dm
C'est un exo basé sur un raisonnement par disjonction des cas :

On aimerait repésenter graphiquement la fonction f(x)=/2x-6/+/x+4/. En fonction de x, /2x-6/ peut avoir deux expression ( quand je met / .. / = valeur absolue )
1er cas : /2x-6/ = 2x-6 si 2x-6 ≥ 0 autrement dit si x≥3
2e cas : /2x-6/= -(2x-6)=-2x+6 si 2x-6<0 autrement dit si x<3

Determiner de la meme facon x+4 en fonction de x
J'ai mis ( je ne suis absolument pas sur ) :
/x+4/ = x+4 si x+4 ≥0 autrement dit si x ≥ -4
/x+4/= -(x+4)= -x-4 si x+4<0 autrement dit si x < -4

Pouvez vous me dire si cela est juste mais sa me semble faux..
Merci d'avance
Berlyn

Bonjour,

C'est bon mais pour trouver les expressions de f(x) ( sans symboles de valeurs absolues ) , il faut ensuite que tu fasses trois cas :

x ≤ -4 , -4 < x < 3 et x ≥ 3 .

Cela constitue la deuxieme question
Je vous dis mes réponses quand j'aurais trouvé !
Merci

pour x<-4 Il faut que je remplace par exemple dans mon expression les x par -4 ?
Je ne comprend pas vraiment
Merci d'avance

Pour x ≤ -4 , necessairement x < 3 donc :

|x+4|=-x-4
|2x-6|=-2x+6

f(x) = (-2x+6)+(-x-4) =....

-2x+6 -x -4 =-3x + 2 ?

oui.

Oki, je n'ai pas tres bien compris votre , necessairement x < 3

Tous les nombres plus petits que -4 sont forcément plus petits que 3

Ok !!
Pour -4≤x≤3 sa donne :
/2x-6/ + /x+4/ = 2x -6 + x +4 = 3x -2 ?

non

Pour -4≤x≤3 :
|2x-6|+|x+4|=(-2x+6)+(x+4)=...

Remarque : si tu as l'habitude , tu peux disposer tes réponses sous forme de tableau ( qu'il faut compléter , bien sûr )
$\begin{tabular} {|c|ccccccccccccc|}\hline x&-\infty&&&-4&&&&3&&&&&+\infty\ \hline (2x-6)&&-&&(-14)&&-&&(0)&&&+\ \hline|2x-6|\\hline (x+4)&&-&&(0)&&+&&(7)&&&+\\hline|x+4|\ \hline f(x)\ \hline \end{tabular}$

Je ne raisonne pas souvent avec un tableau mais merci !!
La reponse est donc tout simplement :
|2x-6|+|x+4|=(-2x+6)+(-x-4)=-3x+2 comme a la réponse précédente..?
( excuser moi je ne cerne pas trop l'exo..)

non.

Pour -4≤x≤3 :

f(x)=|2x-6|+|x+4|=(-2x+6)+(x+4)=.....=-x+10

f(x)=|2x-6|+|x+4|=(-2x+6)+(x+4)=-2x +6 + x + 4=-x+10

Je pense avoir compris !!!
Pour x ≥3 :
f(x)=(2x-6)+(-x-4)=2x-6-x-4=x-10

non

Pour x≥3 ( donc x ≥ -4) :

f(x)=(2x-6)+(x+4)

Ah oui j'avais écris sa sur ma feuille en plus, je suis aller trop vite !!
Merci pour votre aide cela est clair maintenant

Les questions suivantes me semble facile : ( etudier le sens de variation => il n'y a que des fonctions affines) puis tracer la courbe sur [-6;6] encore merci et a bientot !!

C'est parfait si tu as bien compris.

Pour pouvoir vérifier , je te joins un schéma

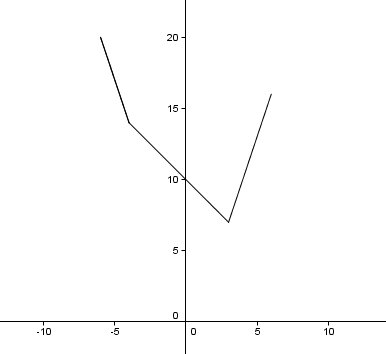
$fichier math$

a+