Ecrire le cout de production unitaire en fonction de x
-
Ccamille60 dernière édition par Hind
Bonjour, dans une entreprise fabricant de la vaisselle, le cout de production unitaire d'une assiette est fonction de la quantité d'assiettes fabriquées par mois. Le cout de production unitaire en euros est donné par la relation : cout=9000/quantité+0,5.
- Pour préserver l'emploi dans l'entreprise, la production ne peut pas être inférieur à 1000 assiettes par mois. Calculer le cout d'une assiette.
f(x)=9000/x+0,5
f(x)=9000/1000+0,5
f(x)=9,5- Quand elle fonctionne à plein régime, l'entreprise produit 7000 assiettes par mois. Quel est alors le cout d'une assiette?
f(x)=9000/x+0,5
f(x)=9000/7000+0,5
f(x)≈1,8Merci de me dire si le calcul est correct avant de faire la représentation graphique.
-
IIron dernière édition par
Bonjour Camille,
Tes calculs me semblent corrects.
Puisqu'il s'agit d'un coût en euros, je donnerais et arrondirais plutôt au centime près, soit 9,50 et 1,79
-
Ccamille60 dernière édition par
Merci je vais arrondir au centime près.
Je dois faire la représentation graphique, je dois donc tracer une droite car c'est une fonction affine?
-
IIron dernière édition par
Ce n'est pas une fonction affine, on pourrait l'écrire sous la forme a(1/x)+b et non pas ax+b
f(x) = 9000 * (1/x) +0,5
Tu devrais obtenir une hyperbole ... une seule branche de l'hyperbole même étant donné son intervalle de définition
Sur quel intervalle vas-tu la tracer ?
-
Ccamille60 dernière édition par
l'intervalle est [1000;7000]
Merci pour votre aide.
-
IIron dernière édition par
Dresse un tableau de valeurs puis trace la fonction en choisissant judicieusement l'échelle.
1000 ; 1500 ; 2000 ; ...
9,5 ; ...exemple :
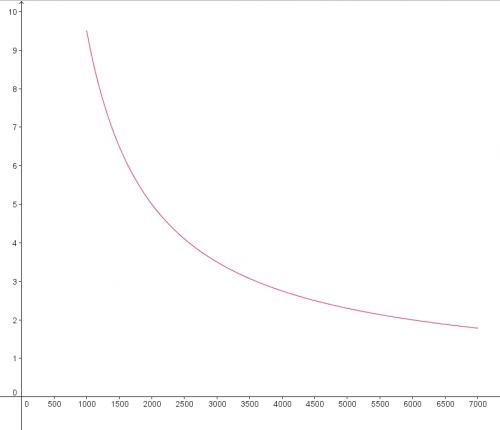
-
Ccamille60 dernière édition par
D'accord je fais un tableau de valeurs qui va me servir à expliquer ma démarche.
J'ai les unités pour le graphique en abscisse : 1cm pour 1000 et en ordonnées : 1 cm pour 1 donc ça va.
Après je dois établir le tableau de variation de la fonction :
x 1,79 9,50
f(x) 7000 1000Je met une flèche au milieu du tableau pour montrer que la fonction est croissante.
Est ce que c'est cela?
MERCI.
-
IIron dernière édition par
L'échelle est OK
camille60
x 1,79 9,50
f(x) 7000 1000Attention, tu confonds abscisses et ordonnées:
x | 1000 .................7000
f(x) 9,50 --flèche vers le ???--> 1,79
Tu es sûre qu'elle est croissante ? Dans quel sens mets-tu la flèche ?
-
Ccamille60 dernière édition par
oui je viens de voir mon erreur, merci.
Donc :x 1000 2000 3000 4000 5000 6000 7000
f(x)9,50 5 3,5 2,75 2,30 2 1,79Donc elle est décroissante, je mets les flèches en vers le bas.
Après je dois déduire l’évolution du cout de production quand la production augmente.
-
IIron dernière édition par
Citation
x 1000 2000 3000 4000 5000 6000 7000
f(x)9,50 5 3,5 2,75 2,30 2 1,79On te demande un tableau de variation (ça, c'est un tableau de valeurs)
Citation
Donc elle est décroissante, je mets les flèches en vers le bas.
OuiCitation
Après je dois déduire l’évolution du cout de production quand la production augmente.
En abscisse : tu as la quantité d'assiettes fabriquées par mois
En ordonnée : le cout de production unitaire d'une assiettePuisque la fonction est ..., quand la production augmente, le coût de production ...
-
Ccamille60 dernière édition par
oui excusez moi pour le tableau de variation, je l'ai mal fait (oublié flèches).
Donc puisque la fonction est décroissante, quand la production augmente, le cout de production baisse.Dernière question : l'entreprise subit des pertes, lorsque le cout de production est supérieur à 6 euros. Quelle doit être la quantité d'assiettes produite par mois pour que le fonctionnement de l'entreprise ne soit pas mis en péril?
Je ne trouve pas quel calcul faire. Merci pour votre aide.
-
IIron dernière édition par
Citation
oui excusez moi pour le tableau de variation, je l'ai mal fait (oublié flèches).
Dans le tab de variation, dans la partie f(x), tu ne mets les valeurs que pour les extrémités de la flècheCitation
Donc puisque la fonction est décroissante, quand la production augmente, le cout de production baisse.Oui
Citation
Dernière question : l'entreprise subit des pertes, lorsque le cout de production est supérieur à 6 euros. Quelle doit être la quantité d'assiettes produite par mois pour que le fonctionnement de l'entreprise ne soit pas mis en péril?l'entreprise ne sera pas mise en péril si :
cout de production est inférieur à 6 euros
f(x) ≤ 6 (inéquation à résoudre)
Tu pourras vérifier ton résultat graphiquement ou à la calculette
-
Ccamille60 dernière édition par
Je ne comprend pas quand vous dites de mettre les valeurs que pour les extrémités de la flèche?
Sinon MERCI pour votre aide, il ne me reste plus qu'à résoudre l'inéquation.
-
IIron dernière édition par
Comme je l'ai noté plus haut
x | 1000 ....................................7000
f(x) | 9,50 --flèche vers le bas--> 1,79
la valeur 9,50 sous le 1000
la valeur 1,79 sous le 7000
-
Ccamille60 dernière édition par
OK encore merci pour votre aide .
-
IIron dernière édition par
Je t'en prie
Il me faut quitter pour ce soir.
Si tu résous correctement ton équation, tu trouveras qu'il faudra fabriquer au moins 1637 assiettes pour rester rentable.
Bonne soirée
-
Ccamille60 dernière édition par
bonne soirée à toi aussi.