Conjectures droite+parabole

[Pierrotile]

Bonjours,
J'ai une etude théorique que je ne comprends pas.
On me demande de créer une figure à l'aide de gégébra.
Donc je créé un curseur m dans l'intervalle [-5;5], je saisis y=x² et y=2x+m
la droite et la parabole se coupent en deux point A et B et C le mileu du segment [AB] Ce qui donne :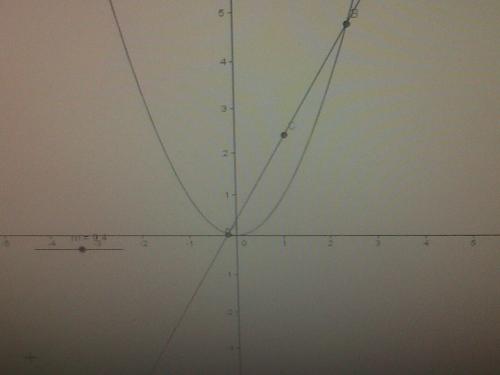

Ensuite on me pause 3 question:
1)Montrer que la parabole et la droite se coupent en deux points distincts ou non si et seulement si m≥-1
2)Calculer les coordonnées de A et B
3) Calculer l'abscisse du point C et démontrer la conjecture sur l'ensemble des points C lorsque m varie.

Ou j'en suis:

1. x²=2x+m
   x²-2x-m=0
   Δ=(2)²-4(-m)
   =4+4m
   =4(1+m)

4(1+m)>0 équivaut à 1+m>0
m>-1

2. x²-2x-m=0
   Δ=4(1+m)
   L'équation a donc deux solution distincts
   2$sqrt$4(1+m)/2=1+$sqrt$(1+m)
   -2$sqrt$4(1+m)/2=1-$sqrt$(1+m)
   Après je bloque.
3. je n'arrive pas a trouver l'abscisse de C

Merci d'avance pour votre lecture.

[mtschoon]

Bonjour,

une remarque pour la 1)

L'énoncé précise "deux points distincts ou non" : Δ ≥ 0 c'est à dire m≥-1

OK pour la 2)

Pour la 3) :

$x_c=\frac{x_1+x_2}{2}$

Tu dois trouver $x_c=1$

Les points C sont donc sur la droite parallèle à l'axe des ordonnées , d'équation x=1