limite ( lecture graphique et calculette )
-
Tterminales dernière édition par
bonsoir à tous
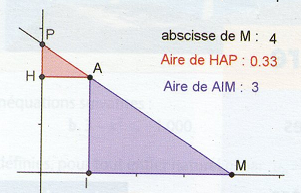
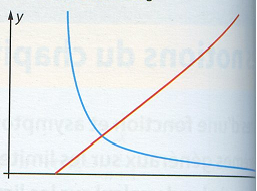
j'ai besoin de votre aide pour mon exercice de mathson note f(x) l'aire du triangle AIM et l'aire du triangle HAP g(x) sur la figue 2 on a representé les fonctions f et g
-
en observant l'évolution de la'ire de HAP lorsque le point M s'approche du point i:
a) reconnaitre la courbe qui represente g parmi les deux courbes données;
b)determiner si possible des valeurs de x strictement superieures à 1 telles que l'aire de HAP est supérieure à 10 -
on admet que l'aire du triangle HAP est egale à 1/(x-1)
construire avec la calculatrice un tableau de valeurs pour la fonction g en partant de x=1,1 avec un pas de -0,01
que peut on dire de l'aire du triangle HAP lorsque x prend des valeurs de plus en plus proches de 1?
je n'arrive pas aux deux questions quelqu'un peut m'aider svp
merci à tous de votre aide
-
-
Tterminales dernière édition par
je comprends pas la question 1)a) quelqu'un peut m'aider svp
-
Tterminales dernière édition par
POUR LA 1 CEST LA COURBE ROUGE MAIS POUR LA JUSTIFICATION
car plus le point m se rapproche de i plus l'aire de hap augmente
c'st bon?
-
Tterminales dernière édition par
pour la 2 plus x se rapproche de 1 plus l'aire du triangle hap augmente
c'est bon?
-
Tterminales dernière édition par
Coucou tout le monde. pouvez vous m'aidez à répondre à la question 1 b car je n'y arrive pas sinon pour la 1 a j'ai répondu la courbe rouge car quand m se rapproche de i l'aire du triangle HAP augmente. pour la 2 j'ai mis mon tableau et j'ai dit que plus x se rapproche de 1 plus l'aire du triangle HAP augmente et dès qu'on arriveà 1 çametserreur syntaxe. voilà merci devotre aide!

-
mtschoon dernière édition par

Bonjour,
Je suppose que A est le point fixe de ta figure A(1,2) et que x est l'abscisse de M
Tu as , je suppose , fait la figure avec un logiciel type "geogebra" pour faire déplacer le point M sur l'axe des abscisses et comprendre ce qui se passe.
Aide pour 1)a)
Lorsque M s'approche de I par la droite ( x tend vers 1 par valeurs supérieures à 1 ), la droite (AM) s'approche de la droite "verticale" passant par A . le point P "monte" indéfiniment sur l'axe des ordonnées don l'aire AHP augmente indéfiniment
Tu conjectures ainsi que :
limx→1+g(x)=+∞\lim_{x\to 1^+} g(x)=+\inftylimx→1+g(x)=+∞
De plus , lorsque M s'éloigne indéfiniment sur l'axe des abscisses vers la droite ( x tend vers +∞ ) , la droite (AM) s'approche de la droite "horizontale" passant par A , le point P s'approche de H , donc l'aire AMP tend vers 0
Tu conjectures ainsi que :
limx→+∞g(x)=0\lim_{x\to +\infty} g(x)=0limx→+∞g(x)=0
Avec ces renseignements , tu dois bien arriver à trouver si g correspond à la courbe rouge ou la courbe bleue
Pour 1)b) , la question n'est que graphique : comme je te l'ai déjà dit , prends un logiciel du type "geogebra" et observe . C'est tout.
Pour x=1 , M est au point de coordonnées (1,0) , la droite (AP) est verticale , l'aire (AHP) n'est pas un nombre ( l'aire tend vers +∞ ) donc il est absolument normal qu'une calculette ne puisse pas faire le calcul numérique pour cette valeur de x...
g(x)=1x−1g(x)=\frac{1}{x-1}g(x)=x−11
L'ensemble de définition de g est R-{1} car x-1 doit être différent de 0 ( on ne peut pas diviser par 0 )
-
Tterminales dernière édition par
Pour le 1 b je sais pas comment répondre j'ai essayé de bouger le point À est m mais je bloque
-
mtschoon dernière édition par

A a pour coordonnées (1,2) : A est fixe. il ne peut pas bouger !
C'est le point M qu'il faut faire déplacer.
-
Tterminales dernière édition par
Je trouve pas aire de HAP supérieur à 10 en bougeant m
-
mtschoon dernière édition par

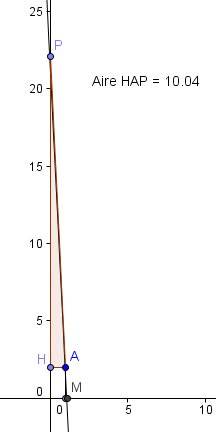
Avec quel logiciel travailles-tu ?
Je te joins une image faite avec géogebra qui sait calculer l'aire d'un triangle.
Pour une aire très légèrement supérieure à 10( 10,04) , tu peut constater que x ( abscisse de M ) est légèrement supérieur à 1 ( environ 1,1 )