Limite de l'aire d'un triangle

Bonjour
Je bloque sur un des nombreux exercices composant mon devoir maison.
Je souhaiterai un petit éclaircissement, si possible
Voici l'énoncé:

Dans un repère orthonormé la fonction f est définie pour x>0 par f(x) = 1/x
De plus a > 1
Les points A et B appartenant à la courbe de la fonction inverse, ont pour abscisses respectives a et 1/a
On note S(a) l'aire du triangle coloré déterminé par les tangentes en A et B à la courbe et l'axe des abscisses.
Etudier la limite de S(a) lorsque a tend vers +∞

Alors je suis partie du principe suivant
On sait que l'aire d'un triangle dont on connait la hauteur et la base vaut : (b*h)/2
D'après ce que j'ai compris la base du triangle est la différences entre les deux tangentes et la hauteur est la perpendiculaire à l'intersection des 2 tangentes coupant l'axe des abscisses.
Est ce que cela est juste ?
Y a t-il un raisonnement plus simple, car je trouve cela un peu complexe !

J'ai donc essayé de calculer la tangente en A:
j'ai trouvé
y= f'(a)(x-a)+1/a
y= -1/a² (x-a) + 1/a
y = (-x+a)/a² + 1/a
y= (-x+2a) / a²
Est-ce juste ?

J'ai ensuite calculer la tangente en B mais je trouve un résultat qui ne me parait pas cohérent:
J'obtiens:
y = ax -1 + a

Si vous pouvez me donner un coup de pouce, ce serait formidable !
Car ce n'est que le premier exercice d'une longue série !
Bonne journée & Merci d'avance !

Bonjour,
Pour la tangente en A, cela me paraît juste.
Mais peux-tu détailler tes calculs pour l'autre tangente ?

Citation
On note S(a) l'aire du triangle coloré déterminé par les tangentes en A et B à la courbe et l'axe des abscisses.Je ne comprends pas ton énoncé : peux-tu joindre la figure ?

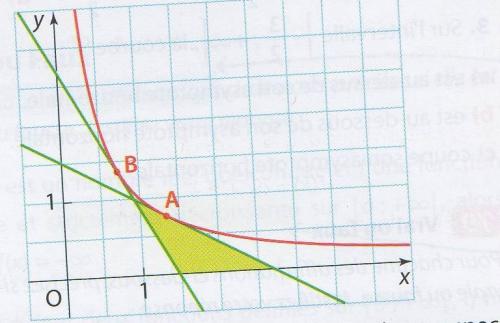
Pour le calcul de la tangente en B j'ai fais:

y = f'(1/a) + (x-1/a) + a
y = 1/(1/a) (x-1/a) + a
y = a ( x-1/a) + a
y = ax - 1 + a

Est ce que cela est cohérent ?

Merci d'avoir répondu si rapidement Mathtous

L'erreur vient du calcul de f '(1/a) :
On a f '(x) = -1/x²
Alors que vaut f '(1/a) ?

Ah d'accord,
alors du coup on a :
f'(1/a) = -1 / (1/a)²
f'(1/a) = -1 * (a/1)²
f'(1/a) = - a²

C'est juste ?

Oui.
Tu peux donc corriger l'équation de la tangente en B.

Super !
Alors je trouve

y = -a² (x-1/a) + a
y = -a²x - 2a

C'est cela ?

Vérifie les signes ...

Oui pardon , j'ai fais une erreur en recopiant sur l'ordinateur
J'ai bien
y = -a²x + 2a
C'est bon cette fois ci ?

Oui.
Pour qu'on se comprenne, nomme les points comme moi :
C : le point d'intersection des deux tangentes
D : le point d'intersection de la tangente en B avec l'axe des abscisses
E : le point d'intersection de la tangente en A avec l'axe des abscisses
(E est donc à droite de D, pour a > 1)

Calcule les coordonnées de ces points.

J'ai fais une figure sur géogébra, pour avoir les mêmes points que vous.
Je calcule les coordonnées et je vous écrit tout ça !

Il suffisait d'écrire les lettres sur le premier dessin.

J'ai du mal à trouver une équation pour le point C
J'ai :
(-x+2a) / a² = -a²x + 2a
-x + 2a = a² ( -a²x + 2a)
-x + 2a = $a^4$ x + $2a^3$
-x = $a^4$ x + $2a^3$ - 2a
x = $a^4$ x - $2a^3$ + 2a

C'est étrange non ?

Tout à fait.
Citation
2a = $a^4$ x + $2a^3$ + x
a = $a^4$ x + $a^3$ + xTu as une curieuse façon de simplifier ! Il n'y a pas de "2" partout.
La première équation est juste : isole x afin de le calculer.

on a donc :
2a = $a^4$ + $2a^3$ + x
2a + $a^4$ x - $2a^3$ = x

Juste ? :rolling_eyes:

Tu n'as pas regroupé les "x" :
2a + $a^4$ x - $2a^3$ = x
$a^4$ x -x = $2a^3$ -2a

Cela se simplifie encore ?

On cherche à calculer x.
$x(a^4$ - 1) = 2a(a² -1)
Et on utilise les identités remarquables.

Je ne comprends pas comment utiliser les identités remarquables ?
Pourquoi faire ça ?

Pour simplifier le calcul de a.
Tu sais que a² - b² = ...
Donc a² - 1 = ...
Mais c'est inutile car on a aussi : $a^4$ - 1 = ?

Alors
a² -b² = (a+b) (a-b)
Donc
$a^4$ - 1 = (a² + 1 ) (a² -1)

C'est ça ?

Si tu veux.
Mais factoriser a² - 1 était (comme je l'ai dit) inutile.
Reviens à ton équation :
$x(a^4$ - 1) = 2a(a² -1)
x(a²-1)(a²+1) = 2a(a²-1)
Et on peut simplifier par a²-1 qui est non nul car a > 1.
On obtient donc x = 2a/(a²+1).
Il te faut y.

Ah oui d'accord j'ai compris pour x !!
Il faut maintenant que je remplace x dans l'équation de ma tangente du départ?

Ah oui d'accord j'ai compris pour x !!
Il faut maintenant que je remplace x dans l'équation de ma tangente du départ?

Oui, si tu tiens absolument à t'appuyer les calculs.
Mais observe bien la figure : pas besoin de calculs pour avoir l'ordonnée de C.

L'ordonnée de C sera la même dans tous les cas?
Même quand a tendra vers + ∞ ?

Citation
L'ordonnée de C sera la même dans tous les cas?Que veux-tu dire ?
L'ordonnée de C n'est pas constante.
L'ordonnée de C est égale à l'abscisse de C, mais pourquoi ?

C'est vrai en effet, mais je n'en ai pas la moindre idée :frowning2:

Tu sais que ta courbe (une demi-hyperbole) admet un axe de symétrie : la droite Δ d'équation y = x (la bissectrice des axes, le repère étant orthonormé)
Les points A et B, situés sur cette courbe, sont symétriques l'un de l'autre (à cause de leurs coordonnées).
Donc leurs tangentes aussi sont symétriques par rapport à Δ.
Par suite, elles se coupent sur Δ pour laquelle y = x (abscisse = ordonnée).

Donc $y_C$ = $x_C$ = 2a/(a²+1)
Tu peux bien sûr vérifier en effectuant les calculs ainsi que tu l'as indiqué.

D'accord j'ai compris !
Merci
On peut alors le justifier ainsi ou en faisant les calculs n'est - ce pas ?
Je vais quand même essayer les calculs

C'est au choix.
Personnellement, j'ai davantage peur des calculs que du raisonnement.

Oui
De toute façon le calcul je ne suis même pas capable de le faire

Ah si !
Tu choisis l'équation d'une des deux tangentes : par exemple
y = 2a - a²x
Tu y remplaces x par 2a/(a²+1) :
y = 2a - a²*2a/(a²+1)
Tu réduis au même dénominateur :
y = [2a(a²+1) - $2a^3$ ]/(a²+1)
Et tu continues seul les calculs.

J'ai fais un peu autrement je crois, j'espère avoir bon
y = 2a - a² x
y = 2a - a² * ( 2a / a² + 1 )
y = 2a - $2a^3$ ) / a² + 1
y = (a²+1 / a² + 1) * 2a - $2a^3$ / a² + 1
y = 2a / a² + 1

C'est bon ?

C'est la même chose.
Attention : le bloc (a²+1) doit être entre parenthèses ici (avec les écritures fractionnaires, ce serait plus simple).
Maintenant, il te faut les abscisses de D et de E.

D'accord Super !
Ca me fait un point dont les coordonnées sont jutes !
Pour l'abscisse de D il faut bien que je résolve
-a²x + 2a = x ?

Non.
y = 2a - a²x, y pas x.
Mais que vaut y sachant que D est situé sur l'axe des abscisses ?

Sachant que D est situé sur l'axe des abscisses on peut dire que y vaut 0
Cest ca ?

Oui, donc 2a - a²x = 0, d'où x = ...

D'où x = 2/a
Juste ?