DM TS tétraèdre régulier

Bonjour, je suis en terminale S et j'ai un devoir maison à faire pendant les vacances, voici l'énoncé :
ABCD est un tétraèdre régulier de côté 1. I est le milieu de [AB] et D' est le centre de gravité du triangle ABC. On appelle médianes du tétraèdre ABCD les droites qui relient chaque sommet au centre de gravité de la face opposée.
Dans la première partie j'ai montré que chaque médiane du tétraèdre est orthogonale à sa face opposée.
Dans la deuxième partie, j'ai montré que les médianes étaient concourantes en un point G et que le vecteur C'D' = 1/3 du vecteur DC (avec C' le centre de gravité du triangle ABD).
Il faut ensuite, à partir de cette relation, démontrer que le vecteur GD' = 1/3 du vecteur DG
C'est ici que je suis bloqué car j'ai beau décomposé le vecteur GD' dans tous les sens avec la relation de Chasles, je n'arrive pas à l'exprimer en fonction du vecteur DG.
Merci de me donner quelques indications pour me mettre sur la voie

Voilà le dessin (fait rapidement sur paint) pour que vous visualisiez mieux :

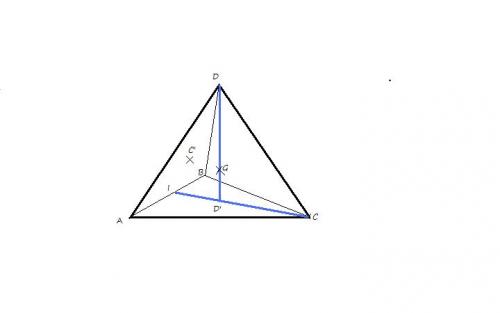
$fichier math$

Bonjour,

Je viens de voir que tu as commencé à dialoguer avec "edualc" ailleurs.

Oui, mais pour l'instant il n'a pas apporté de solution à mon problème. Mais j'espère qu'il pourra m'aider.

Pour t'avancer un peu , vu que tu n'a pas pour l'instant de réponse à la question posée , je regarde un peu.

Si j'ai bien compris , tu as prouvé que $\text{\vec{c'd'}=\frac{1}{3}\vec{dc}$

Tu peux en déduire que les droites (C'D') et (CD) sont parallèles et appliquer le théorème de Thalès aux triangles GC'D' et GCD

$c′d′cd=gd′gd\frac{c'd'}{cd}=\frac{gd'}{gd}$

Or $c′d′cd=13\frac{c'd'}{cd}=\frac{1}{3}$

donc $gd′gd=13\frac{gd'}{gd}=\frac{1}{3}$

Tu obtiens donc ainsi : $gd′=13gdgd'=\frac{1}{3}gd$

$gd′⃗\vec{gd'}$ et $gd⃗\vec{gd}$ sont de sens contraires donc ........... (* tu termines* )

Remarque : continue ton dialogue avec "edualc" , sinon , on ne s'y reconnaitra plus !