position courbes et asymptote

Bonjour à tous !

J'ai un petit problème pour un exo sur les fonctions :

Partie C :

On appelle C la courbe représentative de f(x)= (x^3+1)/(4x^2-1) (définie sur O,5exclus;+infini) et D la droite d'équation y=x/4.

1)a) conjecturer les positions relatives de C et de D.
1)b) pour tout réel x>0,5 , on considère les points M et N d'abscisses x respectivement sur C et D.Que peut-on conjecturer sur la distance MN lorsque x tend vers +infini ?
2) démontrer ces conjectures.

Si quelqu'un pouvait m'aider, svp. merci d'avance !

Bonsoir,

Pour la 1)a) et 1)b) la seule façon est de tracer la courbe et la droite ( pour x > 1/2 , sur ta calculette graphique par exemple )

Losque tu l'auras fait , tu n'auras plus qu'à regarder .

L'as-tu fait ?

Merci pour votre réponse.

Oui, je l'ai fait.
D semble être une asymptote oblique à la courbe C.
La distance MN semble tendre vers O.

Mais le problème, c'est la démonstration. Je n'ai aucune idée...

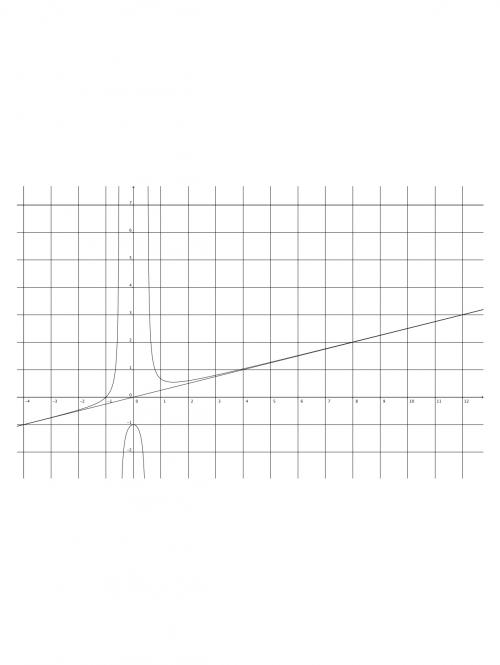
$fichier math$

Ne tenir compte que de la partie de la courbe dans l'intervalle 0,5exclus;+infini.

Très bien .

Tu as dû conjecturer que pour x > 0.5 , la courbe est au-dessus de la droite et que la distance MN tend vers 0 lorsque x tend vers +∞

Piste pour les démonstrations :

$f(x)−x4=x3+14x2−1−x4f(x)-\frac{x}{4}=\frac{x^3+1}{4x^2-1}-\frac{x}{4}$

Tu réduis au même dénominateur , tu simplifies et tu dois trouver , sauf erreur :

$f(x)−x4=x+44(4x2−1)f(x)-\frac{x}{4}=\frac{x+4}{4(4x^2-1)}$

Pour x > 1/2 , tu détermines le signe de f(x)-x/4

Tu dois trouver f(x)-x/4 > 0 donc f(x) > x/4 donc (C) au-dessus de (D)

$mn=f(x)−x4=x+44(4x2−1)mn=f(x)-\frac{x}{4}=\frac{x+4}{4(4x^2-1)}$

Tu cherches la limite de MN lorsque x tend vers +∞ et tu dois trouver 0

Donc**(D) asymptote oblique à (C)**en +∞

Oui, je trouve exactement les mêmes résultats que vous.

Merci beaucoup pour votre aide !!!

Math'piano.

De rien .

A+