Résolution à l'aide du théorème de Pythagore
-
TTitimeli dernière édition par Hind
Bonjour,
J'ai un exercice à faire pour lundi mais je n'arrive pas du tout à répondre aux questions. Voici l'énoncé :On désire installer un élevage de poules dans un bâtiment dont la surface du sol est un rectangle ABCD de dimensions 8 m et 5 m.
Le système de chauffage est assuré par un convecteur infrarouge suspendu au plafond. Le but est de calculer la longueur de fil nécessaire à l'installation électrique.
On appelle X le point au sol situé à la verticale du convecteur.
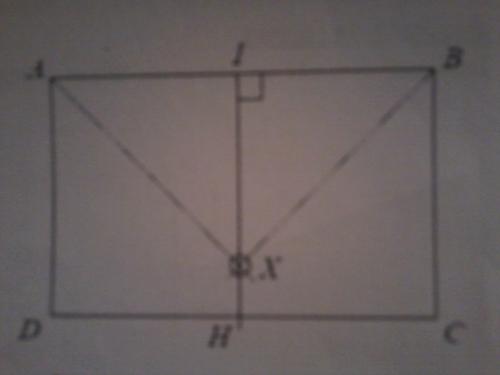
On veut que ce point X soit disposé à égale distance de trois des quatres murs selon le schéma ci-contre.[IH) est la médiatrice du segment [AB].
[AX) et [BX) sont kes bissectrices des angles DAB et ABC du retangle.- Faire une figure à l'échelle 1/100ème (FAIT)
- Justifier que le triangle AIX est un triangle isocèle rectangle en I
- Calculer la longueur AX.
- En déduire la longueur AX + BX.
Merci d'avance.
-
Bonjour Titimeli,
-
Utilise le fait que le point X est à égale distance de trois des quatre murs.
-
Utilise la propriété de Pythagore.
-
-
TTitimeli dernière édition par
Bonjour Noemi,
Pour la 2) j'ai écrit : Puisque X est à égale distance de trois des quatres murs : AX=IX=BX.
Pour la 3) Dans le triangle AIX rectangle en I, on utilise le théorème de Pythagore.
AX²=AI²+IX²
AX²=4²+4²
AX²=16+16
AX²= 32 cm²Longueur AX
AX = √32 cm
Pour la 4) Je ne sais pas comment faire car la longueur AX est une racine carrée.
-
√32 = √(16x2) = 4√2
Comme AX = BX
AX + BX = 2 x 4√2
= ...
-
TTitimeli dernière édition par
Merci pour votre aide. Pour mes réponses de l'exercice, cela donne :
- Figure de la feuille.
- Puisque X est à égale distance de trois des quatres murs : AX=IX=BX.
- Dans le triangle AIX rectangle en I, on utilise le théorème de Pythagore.
AX²=AI²+IX²
AX²=4²+4²
AX²=16+16
AX²= 32 cm²Longueur AX
AX = √32 cm
- AX + BX = √32 + √32
AX + BX = √64 cm
AX + BX = 8 cm.
Ce que j'ai écrit est-il bon pour l'ensemble de l'exercice ?
-
La fin est fausse :
Longueur AX
AX = √32 cm = 4√2 cm
- AX + BX = √32 + √32
AX + BX = 2√32 cm ou 2x4√2
AX + BX = 8√2 cm.
- AX + BX = √32 + √32
-
TTitimeli dernière édition par
D'accord. Merci pour tout.
A bientot.