Résoudre un problème d'optimisation à l'aide des fonctions
-
Yyonel dernière édition par Hind
Bonjour à tou(tes)s, j'ai un dm à rendre pour mercredi mais je bloque sur un problème d'optimisation.
L'énoncé est le suivant :
"Albert est un fervent adepte de la plongée sous-marine. Alors qu'il se trouve en A et s'émerveille devant la beauté du paysage aquatique, il aperçoit un requin d'une taille qui le dissuade de poursuivre plus avant son exploration des fonds marins et décide de rejoindre son bateau situé en B. A quel endroit doit-il rejoindre la surface pour que le temps de parcours soit minimal ?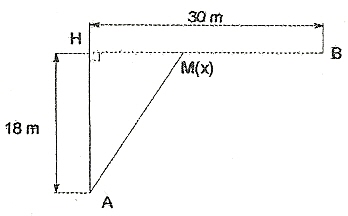
Grâce à l'adrénaline, Albert se déplace à la vitesse de 7.2km/h sous l'eau et à la vitesse de 9km/h en surface. On supposera que la surface de l'eau est rectiligne, que la dérive due au courant est nulle et que la trajectoire d'Albert est une ligne brisée.
On pourra poser HM=x"
Merci d'avance pour votre aide !
-
Cchompchomp dernière édition par
Bonjour,
sympa le problème
- exprimer les distances AM et MB en fonction de x
- exprimer les temps de parcours correspondants en fonction de x (eh oui il y a un peu de conversions à faire)
- ça donne une fonction, il faut chercher son minimum
-
Yyonel dernière édition par
Merci de votre réponse,
AM=√(18²+x²) avec Pythagore
MB=30-x
AM: 7,2 km/h=2 m/s (on divise par 3,6)
MB: 9 km/h=2,5 m/s
Comment exprimer une fonction ?
-
Cchompchomp dernière édition par
C'est ça.
Maintenant le temps de parcours de AM, et celui de BM.
-
Yyonel dernière édition par
AM=√(18²+x²)/2
BM=12-2/5x
C'est ça ?
-
Cchompchomp dernière édition par
Heu presque.
Ce ne sont plus AM et BM mais les temps de parcours en secondes de AM et BM.
Il ne reste plus qu'à trouver le temps de parcours total en fonction de x, on n'a qu'à l'appeler f(x). Et trouver le minimum.
-
Yyonel dernière édition par
f(x)=√(18²+x²)/2 +12- 2/5x
=(5√(18²+x²)-4x)/10 +12
Le minimum est y=18 ?
-
Cchompchomp dernière édition par
Comment trouves-tu le minimum ?
-
Yyonel dernière édition par
Graphiquement pour l'instant
-
Cchompchomp dernière édition par
OK, donc pour la valeur exacte, il faut étudier f (dérivée, tableau de variations).
-
Yyonel dernière édition par
f'(x)=1/(20√(18²+x²)) ?
-
Cchompchomp dernière édition par
Pas du tout

f(x)=1/2 * √(18²+x²) - 2/5x +12
On fait terme par terme.
Et rappel (√u)' = u'/(2√u)
-
Yyonel dernière édition par
√(18²+x²)'=(36+2x)/2√(18²+x²)=(18+x)/√(18²+x²)
(1/2)'=0
(-2/5x)'=-2/5
f(x)'=(18+x)/√(18²+x²)-2/5
C'est ça ?
-
Cchompchomp dernière édition par
√(18²+x²)'=(36+2x)/2√(18²+x²)=(18+x)/√(18²+x²) Non !
18²=324 est une constante, donc sa dérivée est 0, pas 36.(1/2)'=0 oui mais on multiplie par 1/2, donc on ne calcule pas (1/2)'
(-2/5x)'=-2/5 oui
f(x)'=
(18+x)/√(18²+x²)-2/5en rouge ça ne va pas, en vert ça va.Et pour vérifier : http://noombaz.fr/?q=√(18²+x²)
Tu peux même y taper ta fonction complète 1/2 * √(18²+x²) - 2/5x +12
-
Yyonel dernière édition par
D'accord, soit f'(x)=x/(2√(x²+324)) -2/5
Les variations je les étudie bien sur [0;30] ?
-
Cchompchomp dernière édition par
oui
-
Yyonel dernière édition par
Je calcule f'(x)=0 et je trouve x=
x 0 30
f'(x) - Φ +
f(x) Croiss CroissC'est ça ?
-
Cchompchomp dernière édition par
C'est bien ça, je suppose que ton clavier a fourché à la fin :
f(x) DÉCroiss CroissMaintant ça devrait aller pour répondre à la question.
-
Yyonel dernière édition par
Oui désolé.
 donc il doit rejoindre la surface à m de son bateau pour que le temps de parcours soit minimal.
donc il doit rejoindre la surface à m de son bateau pour que le temps de parcours soit minimal.
-
Cchompchomp dernière édition par
Parfait

-
Yyonel dernière édition par
Merci pour votre aide !
Bonne soirée
-
Cchompchomp dernière édition par
À toi aussi
