fonction aire d'arbel

[urian01]

Bonjour, j'ai un exercice à faire mais je ne vois pas comment faire, quelqu'un peut-il m'aider svp.. ?
Exercice :
Un demi-cercle a pour diamètre [AB] avec AB = 6
Un point M est variable sur le segment [AB].
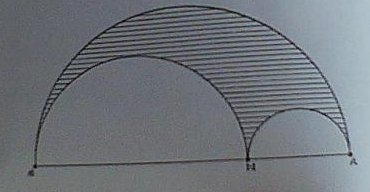
L'arbel est la figure délimitée par les trois demi-cercles de diamètre [AB], [AM] et [BM].
Pour quelle position de M l'aire de l'arbel est-elle maximale ? Quelle est cette valeur aire maximale ?

(Sur la figure les lettres sont B,M,A de gauche a droite

[mtschoon]

Bonjour,

Pistes,

Commence par calculer l'aire de chaque demi-disque

Pour le demi-disque de diamètre [AB] , l'aire vaut
$A_1=\frac{1}{2}\times \pi \times 9$

Pose AM=x , avec 0≤ x ≤ 6
L'aire du demi-disque de diamètre BM vaut
$A_2=\frac{1}{2}\times \pi \times \frac{x^2}{4}$

MB=6-x
L'aire du demi-disque de diamètre AM vaut
$A_3=\frac{1}{2}\times \pi \times \frac{(6-x{)}^2}{4}$

L'aire de l'arbel est donc $f(x)=A_1-(A_2+A_3)$

Tu étudies f pour trouver son maximum.

[urian01]

Merci, j'ai réussi grâce à vous, j'ai enfin compris. Merci beaucoup.

[mtschoon]

De rien.

A+