Discuter par le calcul le nombre de points d'intersection d'une droite et une parabole

Bonjour,
J'ai un dm a faire sur le second degres et geogebra a la fois. Enfaite le but est de faire des conjectures avec geogebra et de les prouver ensuite
Je suis bloquer a la 4) question qui est la suivante :
Disctuer par le calcul le nombre de points d'intersection de (Dm) et de (P)
f(x) = x²-4x+1
(Dm) => y = -2x+m

Il me semble logique de resoudre f(x) = (Dm)
Ce qui donne :
x²-4x+1=-2x+m
x²-2x+1-m=0

Ensuite calcul du delta qui nous donne ∇=4m
Sachant que quand m<0 la droite coupe en 0 point la courbe
m=0 1 point la courbe
m>0 2 point la courbe
Comment prouver cela a l'aide du 4m ? Merci d'avance

Bonjour ,

Je te joins un fichier de géogebra ( qui s'ouvre si ton anti-virus le tolère...)

http://www.geogebratube.org/student/m25486

Fais glisser la droite à la souris.
La valeur de m est l'ordonnée du point d'abscisse 0 de la droite .

Mathématiquement , ton discriminant est juste.

Δ=4m

Trois cas

Δ > 0 <=> 4m > 0 <=> m > 0 : 2 solutions à l'équation qui sont les abscisses des points d'intersection de la courbe avec la droite.

Δ = 0 <=> 4m = 0 <=> m = 0 : .................( tu termines )

Δ < 0 <=> 4m < 0 <=> m < 0 :..................( tu termines )

Bonsoir et merci de votre aide ,

Δ > 0 <=> 4m > 0 <=> m > 0 : 2 solutions à l'équation qui sont les abscisses des points d'intersection de la courbe avec la droite.

Δ = 0 <=> 4m = 0 <=> m = 0 : 1 solutions à l'équation qui est l'abscisse du point d'intersection de la courbe avec la droite.

Δ < 0 <=> 4m < 0 <=> m < 0 : 0 solutions à l'équation donc aucun points d'intersection de la courbe avec la droite.

La question suivante consiste à donner le point d'intersection dans le cas ou il est unique:
Cela correspond donc a quand ∇=0, mais comment s'y prendre afin de trouver le point d'intersection ?
Merci de votre aide

Si tu connais les formules de résolution des équations du second degré , il n'y a pas de problème .

Pour Δ = 0 , c'est à dire m=0 , $x=−b2ax=\frac{-b}{2a}$

Tu peux même éviter d'utiliser la formule avec une identité remarquable .

Pour m=0 , l'éqution s'écrit : x²-2x+1=0 c'est à dire (x-1)²=0 donc x=...

Bonsoir,
Oui merci après reflexion le temps de votre réponse j'ai trouvé la réponse et votre explication renforce mes résultats, je trouve x=1

Et pour l'ordonnée du point de contact , calcule f(1)

Oui et f(1) = 0
La question suivante consiste a faire une conjecture avec Geogebra et ensuite la prouver :
Lorsque (Dm) coupe (P) en deux points disctincs Am et Bm, on appelle Im le milieu de [Am;Bm]. Soit E l'ensemble des points Im quand m parcourt R ( Réel ) tout entier.
a) Construite les points Am et Bm sous geogebra puis Im mileu de Am Bm
b) A l'aide de la fonction trace representer le lieu des points Im
Quel semble etre la nature de l'ensemble E ?
c) Demontrer la conjecture precedente, il faudra donc dans un premier temps determiner les coordonnées des points Am et Bm puis celle de Im

Donc avec la conjecture je trouve que l'ensemble E semble être une demi droite d'équation x = 1 puisqu'elle coupe l'axe des abscices en 1
Mais comment prouver cela .. Les coordonnées de Im sont égales a 1/2 Am et 1/2 Bm mais je bloque pour le reste..
Merci de votre aide

f(1)=0 ? ? ? regarde le schéma et recompte ...

Citation
Les coordonnées de Im sont égales à 1/2 Am et 1/2 Bm

Ta phrase n'est pas claire. La formule doit s'applique séparemmentaux abscisses et aux ordonnées.

$xi=xam+xbm2x_i=\frac{x_{am}+x_{bm}}{2}$

$x_{am}$ et $x_{bm}$ sont les solutions ( habituellement appelées x1 et x2 ) de l'équation su second degré lorsque Δ est positif .

Applique les formules de ton cours pour Δ positif , pour trouver x1 et x2 et simplifie.

x²-2x+1=0
F(1) = 1²-2x1 +1 = 0 , ce n'est pas sa ?
Merci d'avance

Pour les coordonnées on rappel que :
f(x) = g(x) => x² - 2x +1-m
∇=4m

x1= (-b-√∇)/2a
= (2-√4)/2
=0
F(0)= 0²-2x0+1=1

Am( 0;1)

x2= (2+√4)/2
=2
F(2) = 2²-2x2+1
=1

Bm(2;1)

Xi= (0+2)/2=1
Yi= (1+1)/2 = 1

Im ( 1;1)

Voila ce que j'ai fais cela me semble bizzard mais bon, j'attend votre reponse avec impatiente, encore merci

Revois tranquillement l'ensemble car tu mélanges ...

f(x)=x²-4x+1 don f(1)=1²-4.1+1=...

l'équation aux abscisses des points d'intersection est :

x²-2x+(1-m)=0

Δ=4m ( déjà calculé )

Pour m ≥ 0

$x1=2+4m2x_1=\frac{2+\sqrt{4m}}{2}$
$x2=2−4m2x_2=\frac{2-\sqrt{4m}}{2}$

donc .............

Bonjour et merci,

F(x)=x²-4x+1 donc f(1) =2

∇=4m donc :
x1=4m/2=2m
x2=m/2

Cela me donne que l'absice des points je doit donc calculer f(2m) et f(m/2) ? Merci de votre aide

Non...

f(1) ne vaut pas 2 : recompte et de plus , tu peux pratiquement lire le résultat sur le graphique ! ce n'est pas possible de lire 2 . Comprends-tu le graphique ? Demande si la lecture graphique te pose problème.

Non pour x1 et pour x2 : tes simplifications sont inexactes.
Conserve les expressions que je j'ai données et calcule tout simplement $xi=x1+x22x_i=\frac{x_1+x_2 }{2}$

Bonsoir f(1) = -2 ? sinon mon graphique doit etre faux..

Il faut que je simplifie x1 et x2 ou je garde l'expression que vous m'avez donné ?

Merci et désolé, je ne comprend pas vraiment tout la..

Oui f(1)=-2

Est-ce tu peux voir la figure dynamique que je t'ai indiquée ?
Si oui , vérifie
Si non , je peux te mettre une figure fixe.

x1 et x2 ne se simplifient pas beaucoup mais tu n'as même pas besoin de simplifier.

$x1+x2=2+4m2+2−4m2=...=2x_1+x_2=\frac{2+\sqrt{4m}}{2}+\frac{2-\sqrt{4m}}{2}=...=2$

Donc : $xi=x1+x22=22=1x_i=\frac{x_1+x_2 }{2}=\frac{2}{2}=1$

Bonsoir,
Non je n'arrive pas a la voir..

Donc pour la question j'ai formulé comme sa:
Quand m>0 on a 2 solutions a l'equation qui sont :
x1= (2-√4m)/2
x2=(2+√4m)/2

x1+x2= (2-√4m)/2 + (2+√4m)/2
Je barre les racines = 4/2=2
Donc xI= 2/2=1

Mais cela ne me donne que l'abscisse du point, pour l'ordonné il me suffit de faire l'image ?

Encore merci

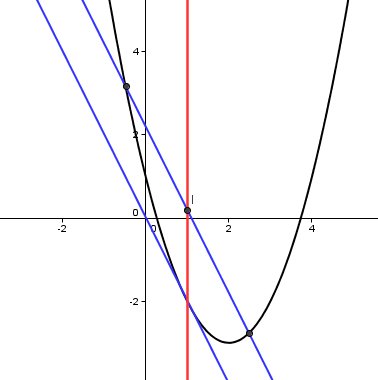
$fichier math$

Les points I sont sur la droite d'équation x=1 ( c'est ce que tu as dû constater graphiquement )

Ok merci j'avais le meme graphique, ma formulation pour la réponse de ma question est donc bonne !
Merci !!

De rien ! Je te conseille de revoir tout cela de près pour bien maîtriser.