Etudier une fonction exponentielle

Bonjour , j'aurais besoin d'aide pour mon exercice Merci

Dans un repère ( ci-dessous) , voici la droite d'équation y=x et la courbe de la fonction g définie sur R par
g(x) = x + 1 – e^x .

a) Lire graphiquement le signe et le sens de variation de g ainsi que les positions relatives de la droite et de la courbe

b) Etudier le sens de variation de g et en déduire le signe de g(x)

c) Etudier par le calcul , les positions relatives de la droite et de la courbe .

pour la a) j'ai dis que le signe de g est négatif , pour le sens de variation que g est strictement croissant de ] - infini ; O ] et strictement décroissant de [ 0 ; + infini [
et pour les positions relatives : j'ai mis que g est plus grand que la droite de
] - infini ; O [ et que g est plus petit que la droite de ] 0 ; + infini [

pour la b) il faut étudier le signe de la dérivée ?

Voilà merci d'avance pour votre aide et Joyeux Noel

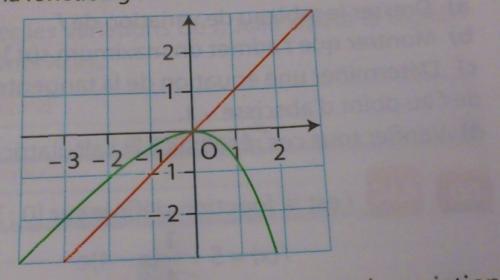
$fichier math$

Bonjour,

Concernant la question a), je suis d'accord avec tes conclusions mais j’écrirais "la courbe représentative de g est au-dessus (puis au-dessous) de la droite".
Pour la question b), on peut effectivement déterminer la dérivée de g puis dresser le tableau de variations.

Cordialement.

Bonsoir homeya ,

pour la dérivée de g c'est bien g'(x) = 1-e^x

c'est ça ?

Oui, c'est bien cela.

d'accord donc j'ai étudier le signe de la dérivée ⇒ elle est positif de
]-infini ; 0 [ et négatif sur ] 0 ; +infini [ et puis j'en ai déduis les variations de g ⇒ g est strictement croissante sur ]-infini ; 0 [ puis strictement décroissant sur ] 0 ; +infini [ .

Pour le signe de g j'ai dis qu'il est négatif car son maximum est 0 .

Voilà c'est juste ?

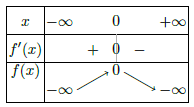
Oui, exactement. Voici le tableau de variations à titre de confirmation. $fichier math$

ok super

pour la c) étudier les positions relatives il faut que je fasse g(x) - y
ou non ??

merci

Oui et donc g(x)-x puis étudier le signe de l'expression obtenue ...

ok donc j'ai calculé g(x)- x et j'ai trouvé -1+e^x
ensuite pour le signe ⇒ négatif de ]-infini ; 0 [ et positif de ] 0; +infini [

c'est juste ? ensuite il faut faire quoi ?

Bonjour,

Le signe est juste mais il faut le démontrer.
il reste à déduire la position relative des deux courbes.

Bonjour Noemi ,

mais comment je peux démontrer le signe , un tableau de signe suffit non ?
je ne vois pas comment avec le signe de g(x)-x je peux déduire les positions relatives

Tu résous l'inéquation $1+e^x$ > 0;

d'accord donc j'ai résolu l'inéquation
-1+e^x > 0
e^x > 1

c'est juste ?

C'est pas terminé
x > .....

mais on peut pas trouver x > ....
parce qu'on peut pas changer l’exponentielle de x : e^x > 1

Tu n'as pas étudié la fonction ln ?
$ln(e^x$ ) = ....

à non pas du tout le logarithme népérien c'est notre prochain chapitre on a pas encore étudier , là je ne connais que l'exponentielle :frowning2:

Donc tu étudies le signe de -1 + $e^x$ en utilisant le signe de g'(x) ou avec celui de $e^x$ .

d'accord donc j'ai étdier le signe de -1+e^x et le signe de g'(x) :

le signe de -1+e^x est négatif de ]-infini;0 [ tandis que le signe de la dérivée g' est positif sur le même intervalle . A l'inverse le signe de -1+e^x est positif de ]0;+infini[ et le signe de la dérivée est négatif sur ce même intervalle

C'est correct.

ok super

En tous cas je vous remercie beaucoup pour votre aide et vous souhaite une très bonne fin d'année

a+