Représenter graphiquement les premiers termes d'une suite et étudier son comportement

Bonjour,
Voila je vous présente mon sujet:
Soit (Un) la suite définie sur N par Uo=4 et Un+1=-2/3Un+5

Representez graphiquement les cnq premier termess de la suite (Un)
La suite (Un) est-elle croissante ? Décroissante ?
Décrire son comportement. (admet-elle une limite, si oui laquelle ? )

Alors voila, pour le 1) je ne vois pas comment peut-on faire pour construire la courbe représentative de f pour pouvoir faire le graphique
Ensuite si vous pouviez me donner des conseils pour le reste

Merci de votre aide.

Bonjour,
Commence par calculer u1,u2,u3,u4
Puis, sur un graphique, tu places les points de coordonnées (n,un). Par exemple, le premier point est le point de coordonnées (0;4).

Un calcul ?
Mais il ne faut pas juste tracer la courbe representative de f et la courbe y=x ?

Ben pourquoi y = x ?
Relis la question :
Citation
Representez graphiquement les cnq premier termess de la suite (Un)Aucun rapport avec ta fonction (y = x).

Ha d'accord j'etais pas du tout partie la dessus merci

Effectue les calculs que je t'ai indiqués, et tu verras tout de suite si la suite est croissante ou autre chose.

Merci beaucoup
Et je ne comprend pas tres bien la 3, peut tu m'expliquer s'il te plai ?

Et donc pour U1 c'est bien 2/3x4+5 ?

As-tu déjà vu que la suite n'est ni croissante ni décroissante ?
On cherche si elle admet une limite.
Vois-tu si $U_n$ se rapproche d'une valeur simple ?

Et donc pour U1 c'est bien 2/3x4+5 ?
Euh je ne sais pas encore

Bonsoir Mathtous.

Je me permets une petite parenthèse...Evidemment , je ne connais pas le cours de Marion...Mais , comme elle parle de la droite d'équation y=x , c'est peut-être bien de la méthode graphique ( qu'elle a vu en cours ) dont-il s'agit...
Elle le dira mieux que moi.

Cela permet de construire les termes de la suite et de conjecturer la limite après avoir construit la courbe $f(x)=−23x+5f(x)=\frac{-2}{3x+5}$ , en repère orthonormé.

Au cas où ce serait cela , je te mets un lien , pour la démarche :

http://www.mathforu.com/cours-93.html

Et bon courage pour l'explication.

Oui voila, je pensais que c'etait cela Modératrice, j'avoue que cette année en maths je suis perdue mais j'aimerais au moins reussir cet exercice

Excuse moi je me suis mal exprimer c'est (2/3)xUn+5

Bonsoir Mtschoon.
Il y a un problème : j'ai sans doute mal lu l'énoncé : je pensais que c'était $U_{n+1}$ = $2/3)U_n$ + 5, mais ce serait $U_{n+1}$ = $2/(3U_n$ +5) ?

non non tu as raison Cosmos

On n'en sortira pas.
Je précise :
$U_{n+1}$ = $2/3)*U_n$ + 5 ?
Un que l'on multiplie par -2/3, puis on ajoute 5 au résultat ?

Mathtous, pas cosmos ...

Dans ce cas, calcule les premiers termes.
Je détaille pour U1:
U1 = (-2/3)U0 + 5
U1 = (-2/3)4 + 5
U1 = -8/3 + 5
U1 = -8/3 + 15/3
U1 = +7/3
C'est bien le calcul qu'il faut faire ?
Ce n'est pas U1 = -2/(34 + 5) = -2/17 ?

oui c'est bien le premier
et pour U2 j'ai trouvé 31/9, c'est beaucoup ...
Pourl les représenter graphiquement sa va etre dur non ?

Citation
et pour U2 j'ai trouvé 31/9, c'est beaucoup ...Compare U1 avec U0, et U2 avec U1.
Compare-les tous avec le nombre 3.
Citation
Pourl les représenter graphiquement sa va etre dur non ?Question de soin : tu vas devoir prendre une unité pas trop petite sur l'axe des ordonnées et utiliser des valeurs approchées.

Maintenant, je suis désolé mais je dois me déconnecter.
A+ si personne d'autre ne te vient en aide .

D'accord et bien je te remercie beaucoup pour ton aide.

Dur , dur , pour comprendre ton énoncé...( Tu avais bien "lu" la bonne formule , Mathtous )

Vu que Mathtous s'ést déconnecté , je continue avec la méthode graphique qui , visiblement, est celle qui est demandée , et avec la formule claire cette fois :

$un+1=−23un+5u_{n+1}=-\frac{2}{3}u_n+5$

Je te mets le schéma que tu dois obtenir mais bien sûr il faut le faire toi-même et le comprendre.

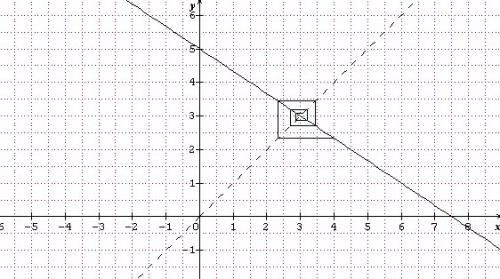
$fichier math$

Pour bien comprendre , tu regardes l'explication avec le lien que je t'ai donné
( explication de Zorro ; la méthode est générale)

http://www.mathforu.com/cours-93.html

En repère orthonormé , tu représentes la fonction f associée : $f(x)=−23x+5f(x)=-\frac{2}{3}x+5$
Tu obtiens tout simplement une droite ( que j'appelle (Cf) )
Tu traces la droite d'équation y=x ( en pointillé sur le graphique que je viens de te mettre ) que j'appelle (D).
Il faut placer les points de construction ( qui ne sont pas fait sur mon graphique ).

Tu pars de U0=4 sur l'axe des abscisses .
Tu "montes" jusqu'à (Cf) : en ordonnée , tu obtiens U1=f(U0)
Grace à la droite (D) , tu repportes U1 sur l'axe des abscisses.

A partir de U1:
Tu "montes" jusqu'à (Cf) : en ordonnée , tu obtiens U2=f(U1)
Grace à la droite (D) , tu repportes U2 sur l'axe des abscisses

A partir de U2:
Tu "montes" jusqu'à (Cf) : en ordonnée , tu obtiens U3=f(U2)
Grace à la droite (D) , tu repportes U3 sur l'axe des abscisses

Tu peus ainsi lire les valeurs de U1 , U2 , U3, ...( qui sont les valeurs que t'a fait calculer Mathous )

Tu peux continuer ce mécanisme graphique indéfiniment , pour conjecturer le comportement de la suite et sa limite lorsque n tend vers +∞ .

Essaie de comprendre et tiens nous au courant.

D'accord sa y est j'ai compris Du coup la droite est décroissante ?
Par contre je n'est pas bien compris la question 3) avec la limite
Je te remercie

C'est bien si tu as compris la manipulation graphique car ce n'est pas facile d'expliquer seulement avec un clavier d'ordinateur...pour un professeur avec un tableau et des élèves en face , c'est plus commode !

la droite est décroissante ?
Si tu parles de la fontion affine f : elle est effectivement décroissante vu que son coefficient directeur es négatif , mas si c'est de la question 2) dont tu parles , ce n'est pas la réponse demandée.

Regarde bien les valeurs U0 , U1 U2 , U3 , U4 ,... sur l'axe des abscisses .

est-ce qu U0 < U1 < U2 < U3 < ...? dans ce cas : (Un) croissante

est-ce qu U0 > U1 > U2 > U3 < ...? dans ce cas : (Un) décroissante

est -ce que U0 > U1 , U1 < U2 , U2 > U3 , ...? dans ce cas (Un ) ni croissante ni décroissante.

As-toi de choisir...

Pour la 3), avec le graphique , imagine la construction de U4 , U5 , U6, ... et essaie de "voir" vers quelle valeur s'approche Un lorsque n augmente indéfiniment.
Tu dois arriver à "voir" cette valeur ( qui sera la limite de la suite , lorsque n tend vers +∞ )

Tiens nous au courant de tes constatations.

La limite c'est vers 3 ?

OUI ! Le graphique te permet de conjecturer que la limite de la suite est 3 ( qui est l'abscisse du point d'intersection de (Cf) avec (D) ).

Si tu ne l'as pas déjà fait , il te reste à conjecturer si la suite (Un) est croissante , ou bien décroissante ou bien "ni croissante ni décroissante" .