variations de fonction
-
Eele17 dernière édition par
Bonjour, pouvez vous m'aidez ?
je cherche le signe de f'(x)= 2+e^-2x+e^2x dans le but d'etudier les variations de f(x)
Pouvez vous m'aidez, car au depart je pensais que c'etait positif mais sur le traceur ca n'est pas uniquement croissant sur R
Merci
-
Vvaccin dernière édition par
Bonsoir
chacun des trois termes est toujours positif ...la conclusion s'impose...
mais est-ce la "bonne" dérivée ?
@+
-
Pptinoir_phiphi dernière édition par
Salut
Comme ∀x∈r\forall x \in \mathbb{r}∀x∈r ex>0e^x \gt 0ex>0
on a donc ∀x∈r\forall x \in \mathbb{r}∀x∈r e−2x>0e^{-2x} \gt 0e−2x>0 et e2x>0e^{2x} \gt 0e2x>0
Conclusion: ∀x∈r\forall x \in \mathbb{r}∀x∈r f′(x)=2+e−2x+e2x>0f'(x)= 2+e^{-2x}+e^{2x} \gt 0f′(x)=2+e−2x+e2x>0
-
mtschoon dernière édition par

Bonjour,
ele17 , je pense que tu mélanges signe et sens de variation .
Si tu as représenté f ' sur ta calculette ( je parle de la fonction dérivée ) , tu as dû trouver cala :
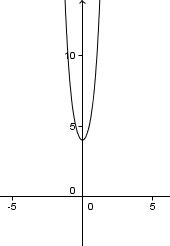
f' n'est bien sûr pas croissante sur R mais elle ne prend que des valeurs strictement positives sur R( le minimum cette fonction dérivée est 4 )