QCM (dérivation et tangente)
-
Gghirlandaio dernière édition par
Bonjour,
J'ai besoin de votre aide à propos de ce QCM, merci d'avance pour aide.QCM (Enoncé) :
Dans les questions suivantes déterminer la (ou les) bonne(s) réponse(s) et justifier. Plusieurs bonnes réponses sont possibles.
-
Soit f la fonction définie sur [smb]R[/smb] par f(x) = −x3−3x2+13\frac{-x^3-3x^2+1}{3}3−x3−3x2+1 et soit Cf sa courbe représentative dans un repère orthogonal. En combien de points de cette courbe la tangeante est-elle parallèle à la droite d'équation y = x ?
a) en 3 points.
b) en 2 points.
c) en 1 point.
d) en aucun point. -
Soit A le point de coordonnées (-5;6) et P la parabole d'équation y = x². Combien existe-t-il de tangentes à P passant par le point A ?
a) une seule tangente.
b) deux tangentes.
c) trois tangentes.
d) aucune tangente. -
La fonction g définie sur [smb]R[/smb]+ par g(x) = x-2[smb]racine[/smb]x est :
a) croissante sur [1; +[smb]infini[/smb][
b) croissante sur[smb]R[/smb]+
c) décroissante sur [0; 2]
d) monotone sur [smb]R[/smb]+ -
Soit u une fonction définie, dérivable et ne s'annulant pas sur un intervalle I. La dérivée de la fonction \frac{1}{u²} est :
a) 12u\frac{1}{2u}2u1
b) −u′2u\frac{-u'}{2u}2u−u′
c) −2u′u3\frac{-2u'}{u^3}u3−2u′
d) 12uu′\frac{1}{2uu'}2uu′1 -
Soit a et b deux nombres réels positifs tels que a+b = 1. La valeur maximale du produit ab est :
a) 1
b) 14\frac{1}{4}41
c) 2
d)12\frac{1}{2}21 -
On donne ci-dessous la représentation graphique de la dérivée de la fonction f.
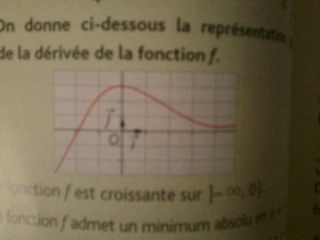
a) La fonction f est croissante sur ]-[smb]infini[/smb], 0].
b) La fonction f admet un minimum absolu en x = -1.
c) La fonction f admet un maximum absolu en x = 0.
d) f(4)<f(2)Ce que j'ai fait :
Réponses
118) Je sais pas...
119) a) une seule tangente (l'axe des abscisses) mais comment justifier ?
120) b) Croissante sur R+
121) Je pense que la réponse est négative mais je ne sais pas laquelle..
122) Je n'ai pas bien compris ?
123) La c et la dJ'ai beaucoup de mal à justifier... En fait, je ne sais pas comment justifier
-
-
SShloub dernière édition par
Salut,
-
A quelle condition deux droites sont parallèles ?
-
L'axe des abscisses passe par A ?
-
Quelle est la valeur en 0 ? En 1 ?
-
Je pense que le signe dépend de u, tu ne connais pas de formule pour calculer la dérivée d'une fonction composée ?
-
On sait que a+b=1, par exemple a=0.9 et b=0.1 (alors ab=0.09) ou a=0.25 et b=0.75 (alors ab=3/16). Quelle est le plus grand ab possible ?
-
Quelle propriété la dérivée vérifie-t-elle pour un minimum ou maximum ?
-
-
Gghirlandaio dernière édition par
Je viens de relire le topique, là où il y a un ?, c'est le "²" pour le 128.
- Quand elles ont le même coefficient directeur ?
- Non pas du tout. Comment je peux savoir ?
- O et -1
- J'ai regardé mon cahier, le carré me perturbe. Il faut que je passe de 1/x à -(a)/(2Vx) ?
- C'est la réponse a) 1 ?
- L'extremum ?
-
SShloub dernière édition par
-
Ok, quel est le coefficient directeur de la tangente à une courbe en un point ? Quel est le coefficient pour y=x ?
-
Tracer la courbe et le point A t'aideront peut-être. Pour commencer, trace quelques tangentes à la courbe pour x>0. Combien de tangentes passeront par A pour x>0 ?
-
Alors ? La fonction est croissante sur R⁺ ?
-
De quel a tu parles ? Par ailleurs, tu n'as pas une formule pour dériver un produit et un quotient ?
-
Quelles valeurs de a et b donnent ab=1 ?
-
Je ne suis pas sûr que tu fasses le bon lien entre la fonction et la dérivée. Que signifie une dérivée positive pour la fonction ? Que signifie un exetremum (de la fonction) pour la dérivée ?
-
-
Gghirlandaio dernière édition par
- Heu justement, je sais pas comment on le calcule.
 J'ai vu cette méthode sur le net : http://fr.answers.yahoo.com/question/index?qid=20110427045053AA8Tx2P
J'ai vu cette méthode sur le net : http://fr.answers.yahoo.com/question/index?qid=20110427045053AA8Tx2P
Mais c'est dur de calculer f(x) avec f'(x)...
Je sais que f'(x)= -x²-2x - Non, elle est décroissante ?
- De u/v à (u'v-uv')/(v²) ?
- 1*1 ?
- En gros, dans ma leçon j'ai juste si f est croissante alors f' est positive.
Pour moi, c'est le sommet de la courbe.
- Heu justement, je sais pas comment on le calcule.
-
SShloub dernière édition par
-
Dit de manière simple, le coefficient de la tangente à la courbe de la fonction f au point x c'est f'(x). C'est quasiment la définition de la dérivée : la pente au point considéré.
-
Oui, de manière plus générale, quel outil connais-tu pour étudier les variations d'une fonction ?
-
Ça me semble correct. Quel est le u et quel est le v ici ? Que valent u, u', v, v' ?
-
Je ne doute pas que a*b=1 pour a=1 et b=1, par conte je doute que a+b=1.
-
On est d'accord. Que dire de la d) ?
Pour ce qui est de l'extremum, c'est en effet un sommet sur la courbe. Mais la courbe de la fonction, pas de sa dérivée. Par contre pour un extremum, la dérivée s'annule (en effet si elle était positive elle ne doit pas continuer, par exemple).
-
-
Gghirlandaio dernière édition par
- Du coup, comment on sait en combien de points la tangente est // avec f'(x)= -x²-2x ?
- Calculer delta et tout ça ?
- Alors u' = 0 et v' = 2u donc ... Réponse c !!
- Quelle méthode je peux faire pour trouver ? Je peux pas justifier par la devinette ?
- Pour la d, f(4) est bien inférieur à f(2), je le vois sur la courbe mais je n'arrive pas à le justifier.
-
SShloub dernière édition par
- Posons g(x)=x. En combien de x on a f'(x)=g'(x) ?
- Je pense à autre chose. Pour rappel, on parle de dérivation ici.
- v' = 2u ? Attention, u est une fonction. Quelle est la dérivée de fg ? De ff ? De u*u ?
- Quelle est la valeur de b en fonction de celle de a ? Remplace b par cette valeur dans l'expression f(a)=a*b. Tu peux ensuite étudier les variations de f entre 0 et 1.
- Une fois de plus, n'oublie pas que c'est la dérivée qui est représentée. Quelle est le signe de la dérivée entre 2 et 4 ? Que cela signifie pour la fonction f ?
-
Gghirlandaio dernière édition par
C'est bon la 118, je l'ai réussi.

- Je ne sais pas.

- C'est étrange, avec la méthode que j'avais mise tout en haut, j'obtiens pourtant la réponse c ? (0*(u²) - 1* (2u))/((u²)²) = (-2u)/u^3)
Par contre je sais pas pourquoi on met le "prime" sur -2u - b= 1-a ?
- Ah oui la dérivée... Si tu parles de x=2 et x=4, elle est décroissante ?
- Je ne sais pas.
-
SShloub dernière édition par
-
Pour étudier les variations, on étudie souvent le signe de la dérivée.
-
Je pense que tu as mal appliqué la méthode. On a v=u*u avec u une fonction. Donc v' = ?
-
Oui, continue.
-
Oui.
-
-
Gghirlandaio dernière édition par
- Je dois dériver g(x) et voir ce que devient delta ?
- Je comprends pas trop...
- Comment j'étudie les variations ?
- Je dois justifier comment après ?
(Désolée d'être un cas)
-
SShloub dernière édition par
- De quel delta tu parles ?
- Tu as une formule pour (U/V)'. Elle dépend de U' et V', il faut donc les calculer.
- En étudiant le signe de la dérivée ?
- Le signe de la dérivée avant -2 justifie la a), le signe de la dérivée en 0 et -1 justifie la b) et la c), le signe de la dérivée entre 2 et 4 justifie la d).
-
Gghirlandaio dernière édition par
- Je parlais du delta de la fonction dérivée ?
- Alors, j'ai regardé dans mon cahier de leçon. Pour les fonctions, j'ai juste la fonction f 1/v qui se dérive en - (v')/v² ou la fonction f u/v qui se dérive en (u'v-uv')/v2. Rien d'autres...
- Si je dérive b= 1-a , j'obtiens b = -1 ? Oo
- Oui mais je ne sais pas f = ?. Je justifie comment graphiquement ?
-
SShloub dernière édition par
- Je ne vois pas de delta, calcule la dérivée et on verra.
- «1/v qui se dérive en - (v')/v²». D'accord, on peut partir de ça. Pour ne pas confondre avec le v de l'énoncé, disons 1/V se dérive en - (V')/V². Pour calculer V', je pense que tu vas utiliser la formule (fg)'=f'g+fg'.
- Ce n'est pas b qu'on dérive, c'est f(a)=a*b
- Tu n'as pas besoin de la valeur exacte de f. Tu peux dire à chaque fois si la courbe de f' est sur l'axe des abscisses (=0), au-dessus (>0) ou en-dessous (<0).
-
Gghirlandaio dernière édition par
- g'(x) = 1 -(2/2Vx) ?
- Je ferai la suite plus tard...
- Je dois faire comment alors ?
- D'accord !

-
SShloub dernière édition par
-
D'accord, tu peux simplifier et étudier le signe.
-
Tu dérives f(a)=a*(1-a). C'est un polynôme, tu peux développer si tu veux.
Tu peux aussi étudier directement cette fonction (polynôme simple, un graphique peut t'aider).
-
-
Gghirlandaio dernière édition par
- Comment je fais pour étudier le signe de x-1 ?
- a-a²
Comment ça ?
-
SShloub dernière édition par
-
Pourquoi x-1 ? Sinon x-1 est une fonction affine, il faut trouver si elle est croissante ou décroissante, puis pour quelle x elle s'annule.
-
Tu vois le coefficient -1 devant a². C'est donc une parabole avec "la tête vers le haut", si tu as étudié ce genre de polynômes en cours, tu peux quasi-directement dire en quelle valeur elle est maximale.
Sinon, tu dérives et regardes quand la dérivée s'annule.
-
-
Gghirlandaio dernière édition par
- g'(x) 1-(1/√x)= (x-1)/√x ?
- Si je la dérive :
1-2a
Et comment je sais quand la dérivée s'annule ?
-
SShloub dernière édition par
-
En l'occurrence, il nous faut juste le signe, résous 1-(1/√x)>0, par exemple.
-
Résous 1-2a=0
-
-
Gghirlandaio dernière édition par
-
Heu comment je fais pour résoudre ? ^^"
-
a=1/2
Ah bah oui ça donne la réponse !!
-
-
SShloub dernière édition par
1-(1/√x)>0 <=> 1>(1/√x) <=> √x>1 <=> ?
-
Gghirlandaio dernière édition par
x >√1 <=> x>1 ?
-
Gghirlandaio dernière édition par
C'est la réponse A alors ?
-
SShloub dernière édition par
Ton raisonnement paraît assez suspect mais x doit être supérieur à 1, oui.
Je pense en effet que A est la bonne réponse.
-
Gghirlandaio dernière édition par
Si x>1, la fonction est croissante sur [1; +infini] non ? Pourquoi est-ce suspect ?
-
SShloub dernière édition par
C'est le passage √x>1 <=> x >√1 que je trouve formulé bizarrement.
Par exemple, √x>2 <=> x >√2 n'est pas vrai.
-
Gghirlandaio dernière édition par
Tu aurais fait comment ?
-
SShloub dernière édition par
Par exemple √x>1 <=> x>1² <=> x>1
-
Gghirlandaio dernière édition par
Ah mais oui ! Ca devient au carré l'autre côté !
Bref, merci pour tout ce que tu as fait !
-
SShloub dernière édition par
De rien, note que cette démonstration serait incorrecte pour un nombre négatif.