Calculer la dérivée d'une fonction et donne ses tableaux de signes et de variation

Bonjour à tous,

Une entreprise créée en janvier 2010, vend des GPS. A la fin du mois d'octobre, le directeur décide d'étudier l'évolution de l'activité de l'entreprise. Le service comptable informe le directeur que le nombre de GPS vendus chaque mois par son entreprise peut être modélisé par la fonction f définie par :

f (x) = −65x² +910x +1400

Où x désigne le rang du mois de l'année 2010

Déterminer f ′(x) où f ′est la fonction dérivée de f sur l'intervalle [1 ; 12] et vérifier que f ′(x) = 130(7−x).

f(x)= -65x² + 910x + 1400
f'(x)= -65 * 2x + 910
f'(x)= -130x + 910

Étudier le signe de f ′(x) sur l'intervalle [1 ; 12].

f'(x)= -130x + 910
Je ne vois pas pour f'(x)=(x - x1)(x - x2) et si je ne trouve pas cela je peux pas continuer pour la suite, merci pour votre aide

Dresser le tableau de variations de la fonction f sur l'intervalle [1 ; 12].
En déduire le mois au cours duquel la vente de GPS est maximale.

Bonjour,
f'(x) = 130(7-x).
Ici, il n'y a qu'une seule valeur de x annulant la dérivée. C'est donc plus simple qu'avec deux valeurs.
Il suffit de placer la ligne 7-x dans le tableau.

Bonjour,

donc pour le tableau:

x 1 7 12

signe + 0 - 0 +
de f'

Non : il n'y a qu'une seule valeur de x annulant f' !
Et sur ton tableau, on voit deux fois 0.

Donc:

x 1 7 12

signe + 0 +
de f'

Le 0 est sous le 7 ?
Mais la dérivée n'est pas tout le temps positive.
As-tu fait une ligne avec 7- x ?
Choisis des valeurs particulières pour t'aider :
quel est le signe de f'(1) ? celui de f'(12) ?

Oui le 0 et sous 7 mathtous
le signe de f'(1) est + et pour f'(12) donc je refais le tableau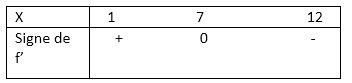

$fichier math$

Parfait.
Complète avec les flèches indiquant les variations de f.

Pour la question 3

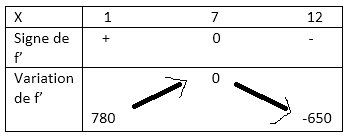
$fichier math$

Non : tu confonds f et f '
Regarde ton tableau : 780 serait plus petit que 0 !!
Les signes de f ' te donnent les variations de f , pas de f '.
Tes flèches sont celles de f.
Et les valeurs 780 et -650 n'ont pas à être calculées.
A la rigueur, tu peux calculer f(1) (pas f '(1)) et f(12), mais ça ne sert à rien.
Corrige ton tableau, il va te permettre de répondre à la question 4.

Et donc pour la question 4:

On en déduis que c'est à partir du mois de janvier que la vente de GPS est au maximum jusqu'au mois de juillet

Non : elle augmente de janvier (mais n'est pas encore maximum) à juillet, est maximum en juillet, puis elle décroît.

Oui c'est vrais pas très logique ce que j'ai fait là

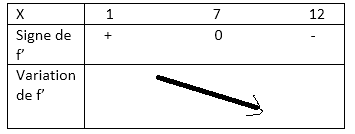
$fichier math$

Mais non. Je t'avais dit que dans ton précédent tableau, les flèches concernaient f, pas f '.
Mais ces flèches étaient correctes pourvu qu'elles s'appliquent à f.
Regarde ton nouveau tableau : les ventes ne feraient que décroitre, alors qu'elles augmentent d'abord, passent par un maximum en juillet (x=7), puis décroissent ensuite.
Et je te rappelle ce que j'ai déjà dit : les signes sont ceux de f ', les flèches c'est pour f (tu écris variations de f ' au lieu de variations de f).
Lis soigneusement ce que j'écris ou on n'en sortira pas.

D'accord merci mathous donc je corrige pour de bon:

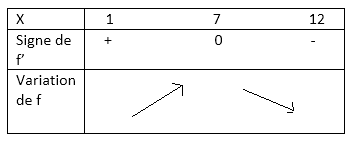
$fichier math$

Cette fois c'est juste.
Tu vois que ça augmente , passe par un maximum (en juillet), puis ça diminue.
Mais place bien les signes entre 1 et 7 , et entre 7 et 12, et pas seulement sous 1 et sous 12.

D'accord merci mathous,

J'ai un autre exercice du même type, je refais un new topic ou je continue là mathous ?

De rien.
Non : il faut faire un nouveau topic (avec un nouveau titre).

D'accord merci mathtous