une aire comme limite d'une suite

bonjour,
voila mon exo
Sn=(1/n+1)+(1/n+2)+...+1/2n
montrer que la suite est croissante et que pour tout nombre entier n≥1, Sn≤1
pouvez vous m'aider si vous plait merci d'avance

Bonjour,

Quelques pistes,

Pour montrer que la suite (Sn) est croissante , tu calcules $S$ _{n+1} $S_n$

Tu trouveras une expression en fonction de n positive

Vu le titre que tu donnes , tu connais "aire et calcul intégral".

Tu fais l'interprétation de la suite avec les aires.

Pour comprendre , je te mets un schéma simple en prenant seulement n=2 et la fonction f définie par f(x)=1/x:

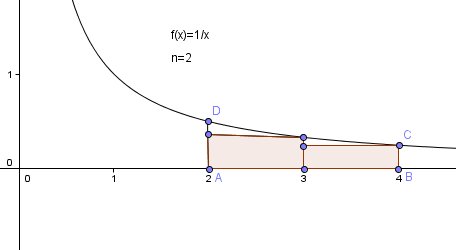
$fichier math$

S2 est l'aire de la zone rosée
S2 est inférieure à l'aire du quadrilatère curviligne ABCD :

$s_2 \le \bigint_2^4 \frac{1}{x}dx$

Tu généralises cette idée à Sn , tu calcules l'intégrale correspondante qui te donnera une valeur inférieure à 1

ok s'est bon j ai réussi merci beaucoup

De rien

A+